Réponse: Le nombre de triangles peut être n'importe quel nombre pair positif sauf 2.

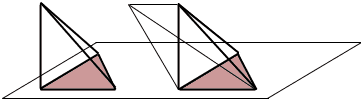
Alexander Potapenko (de Russie) montre comment construire un polyèdre à n+2 faces triangulaires à partir de n'importe quel polyèdre a n faces triangulaires: On ajoute un point à une des faces, et on le connecte par des lignes aux trois sommets de cette face. On a alors trois triangles plutôt qu'un. Ensuite on déplace ce point vers l'extérieur. On a alors trois faces plutôt qu'une. Ainsi, à partir du tétraèdre (qui a 4 faces triangulaires), on peut utiliser ce processus pour obtenir 6 faces, puis 8, puis 10, etc.

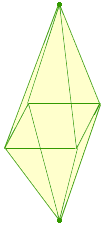
Penny Nom (de Regina) nous a soumis une construction qui fonctionne pour n'importe quel nombre pair de faces sauf 2 et 4: A partir d'un polygone régulier à n cotés, dans un plan horizontal, on ajoute un point au dessus et un point au dessous du centre du polygone, et on joint chacun de ces points aux sommets du polygone. On obtient un polyèdre qui a 2n faces triangulaires qui est symétrique par rapport au plan horizontal.

Chacune de ces constructions montre que n'importe quel nombre pair positif sauf 2 est possible. Penny a ensuite démontré que les nombres impairs sont impossibles. Considerons un polyèdre à n faces triangulaires et comptons le nombre d'arêtes. Chaque triangle contribue 3 arêtes au total, mais chaque arête borde 2 faces, et est comptée 2 fois. Donc le nombre d'arêtes est 3n/2. Puisque ce nombre est un entier, 2 doit diviser 3n sans reste, ce qui implique que n est pair. Ainsi, le nombre n de faces du polyèdre est pair.