Toutes les solutions soumises font usage des deux mêmes
étapes de base, bien que chacune aie sa saveur particulière.
La solution que voici illustre les différentes approches
au problème, et combine les travaux de
Jeff Eggen (Regina)
Normand Laliberté (Ontario)
Leti Gimeno (Espagne)
Juan Mir Pieras (Espagne)
Alexander Potapenko (Russie)
Étape 1: Calcul de la hauteur de A à BC.
(a) Première approche
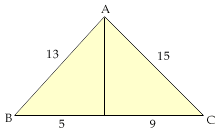
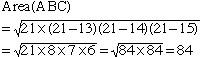 .
.
D'autre part puisque la base BC est 14, la hauteur correspondante doit être 84/7 = 12.
donc BH = 5 et AH = 12. Notez que cette approche justifie algébriquement l'observation faite en (a).
Étape 2: Calcul du côté du carré en se servant de la
similarité entre ADG et ABC.
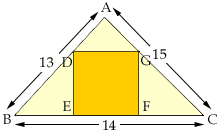
Soit x, le côtédu carré inscrit: x = DE = EF = FG = DG
(a) Première approche (Eggen, Potapenko, Laliberté)
et
Ces rapports étant égaux, on a 12-x/x = 12/14. ce qui donne x = 84/13. En fait, Eggen et Laliberté trigonométrie, ce qui mène à un calcul similaire.
= Aire(ADG) + [Aire(BED) + Aire(GFC)] + Aire(DEFG)
= (1/2)x(12 Ð x) + (1/2)x(14 Ð x) + x2
= 13x
d'où x = 84/13.
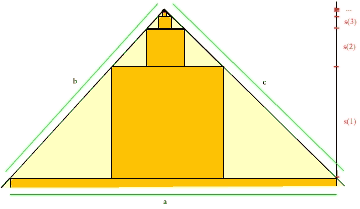
On considére une suite infinie de triangles, chacun avec un carr´ inscrit. Le triangle ABC avec son carré DEFG de côté x sont réduits par un facteur k, résultant en le triangle ADG et son carré de côté kx, qui sont à leur tour réduits par un facteur de k, et ainsi de suite. Cette suite de carrés recouvre entièrement la hauteur du triangle; on a donc
= x + kx + k2x + ...
= x(1 + k + k2 + ...)
= x/1 - k
Par suite, on note que la reduction originale applique le côté BC du triangle, de longueur 14, sur le côté DG du carré, de longueur x. Ainsi, 14k = x et k = x/14, d'où
ce qui donne encore une fois x = 84/13.