Nous avons reçu quatre jolies solutions ce mois ci. Les voici en ordre alphabétique.
- Solution de Leticia Gimeno (Espagne).
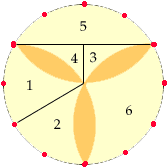
On trace trois rayons joignant le centre aux points 12:00, 4:00 et 8:00 de l'horloge. On obtient ainsi six triangles curvilignes, chacun avec un côté droit, un côté convexe et un côté concave. On en prend deux et on les dispose de façon à ce que le côté convexe de l'un s'emboîte dans le côté concave de l'autre, comme ci-bas. On observe que les côtés droits des deux morceaux sont alors parallèles. C'est un bon début.
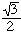 par 3).
par 3).
-
Solution by Normand Laliberté (Ontario).
À montrer: Un rectangle de hauteur
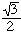 et de largeur 3 peut être formé.
et de largeur 3 peut être formé.
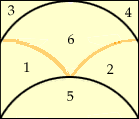
Dénotons par 0 le centre du cercle unité. Notez que les segments 0-10, 0-8, 0-6, 8-10, 6-8 sont tous de longueur 1 en tant que rayons de l'un ou l'autre des cercles utilisés dans la construction. Notez aussi que l'arc de cercle sous-tendu par la corde 8-10 est égal à l'un ou l'autre des deux arcs de cercle, partie ombrée, sous-tendus par la corde 0-10. Donc, en coupant le long de la corde 8-10 et en faisant pivoter l'arc sous-tendu autour du point 10, on arrive a couvrir l'arc ombré sous-tendu par 0-10, et on obtient un triangle équilatéral de sommets 0, 8 et 10.
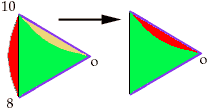
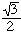 et de largeur 3.
et de largeur 3.
- Solution de Juan Mir Pieras (Espagne)
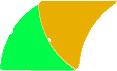
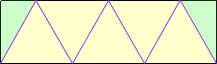
Une construction sans mots! [Notez les dimensions
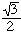 par 3/2]
par 3/2]
- Solution d'Alexander Potapenko (Russie)
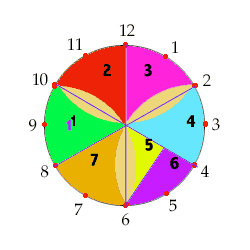
On relie le centre du cercle aux "heures paires" (2, 4, 6, 8, 10, 12) par des segments. On obtient 6 régions, ou, si l'on coupe les segments circulaires, 6 triangles équilatéraux. (Un segment circulaire est une figure délimitée par une corde du cercle et l'arc sous-tendu par celle-ci.) Il est facile de démontrer que chacun de ces segments circulaires est égal a un segment ombré dans chaque triangle (même rayon et base). Ainsi on peut mettre les segments coupés dans les segments ombrés. Ainsi la figure est transformée en 6 triangles équilatéraux. Il est facile de les recombiner en rectangle, simplement en les alignants et en bissectant l'un d'eux (comme dans la solution 2).
Note. Nous avons tiré ce problème de
"Which Way Did the Bicycle Go ?" [Où est allée la bicyclette?]
par J.Konhauser, D.Vellerman et S.Wagon (publié par
The Mathematical Association of America). Leur solution
nécessite seulement six morceaux, ce qui est probablement le minimum
possible. Ça ressemble à la solution 3, mais avec moins de coupes: