Normand Laliberté (Ontario) et Juan Mir Pieras (Espagne) ont recours à des arguments semblables pour démontrer que
du triangle sont soit toutes identiques ou toutes différentes.
Pour N=0, le mot initial a longueur 30 + 1 = 2 lettres, et l'assertion est vraie par définition. Il est pratique de remplacer les lettres A, B, C par les entiers modulo 3. Selon l'arithmétique modulaire, la règle devient alors
Observons comment ce processus opère dans le cas du mot
x0x1x2x3 de quatre lettres:
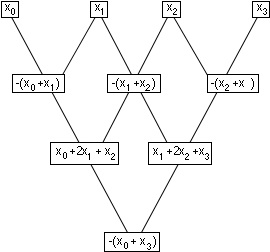
Ainsi, le nombre -(x0 + x3) au bas du triangle ne dépend que des deux nombres x0, x3 des coins du haut du triangle. Tel que noté plus haut, x0, x3 et -(x0 + x3) sont soit tous identiques, soit tous différents.
Pour adapter ce calcul à notre démonstration par induction, il
suffit de remarquer que le triangle de hauteur 31 + 1 = 4 se décompose
en 6 triangles emboîtés de hauteur 30 + 1 = 2.
On généralise cette décomposition au triangle de hauteur
3K+1 + 1, qu'on divise en six triangles emboîtés de hauteur
3K + 1.
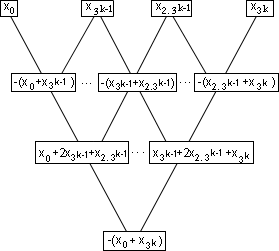
Ainsi, lorsque le mot du haut est x0, x1, ..., x3K+1, on retrouve -(x0 + x3K+1) au bas du triangle. Ceci complète la démonstration de l'assertion (*), selon laquelle pour toute valeur de N, les lettres aux coins du triangle sont soit toutes identiques ou toutes différentes.
Il reste à démontrer que pour toute autre hauteur de triangle, la même conclusion n'est pas valide. Pour ce faire, le plus simple est de se référer à la figure précédente et de donner une suite de contre-exemples pour toutes les hauteurs intermédiaires entre 3K + 1 et 3K+1 + 1.
Il reste à démontrer que pour toute autre hauteur de triangle, la même conclusion n'est pas valide. Pour ce faire, le plus simple est de se référer à la figure précédente et de donner une suite de contre-exemples pour toutes les hauteurs interm\'ediaires entre 3^K + 1 et 3K+1 + 1.
Puisque le mot ABA de trois lettres donne C au bas du triangle. La figure précedente montre que tout mot de 2.3K + 1 lettres dont la première est A, celle du millieu est B et la dernière est A donne C au bas du triangle. En particulier ceci démontre que l'énoncé (*) est faux pour les triangles de hauteur 2.3K + 1.
Considérons un triangle de hauteur 3K + 2, au haut duquel est placé un mot commençant par AA et se terminant par CA. Alors la ligne suivante est un mot de 3n-1 + 1 lettres commençant par A et se terminant par B, et par conséquent la lettre C est au bas du triangle. Ceci démontre que l'énoncé (*) est faux pour les triangles de hauteur 3K + 2.
De même, dans un triangle de hauteur 3K + 3 au haut duquel est placé un mot commençant par AAA et se terminant par BAA la deuxième ligne est un mot de 3K + 2 lettres commençant par AA et se terminant par CA, et par conséquent la lettre C est au bas du triangle. Ceci démontre que l'énoncé (*) est faux pour les triangles de hauteur 3K + 3.
Continuant ainsi, on se rend compte que pour toute hauteur de triangle allant de 3K + 2 à 2.3K, il est possible de placer au haut un mot dont la première et la dernière lettre est A, de telle sorte que la lettre C apparaisse au bas du triangle. Ceci démontre que l'énoncé (*) est faux pour toutes ces hauteurs.
Par suite, il est possible de traiter les triangles de hauteur 2.3K + à 3K+1 de la même façon que les triangles de hauteur 3K + 2 à 2.3K. Dans tous les cas on se rend compte que les deux lettres des coins du haut peuvent être identiques et différer de la lettre du bas. En faisant pivoter le triangle de 120 degrés, on remarque aussi que la lettre du bas peut coïncider avec une des lettres des coins du haut sans que les trois lettres des coins ne soient identiques.
On donne maintenant la solution de Juan Mir Pieras à cette partie
du problème. Il a redécouvert par lui-même un théorème
de Kummer (1852) avec quelques conséquences remarquables.
Kummer s'intéressait à la plus grande puissance p^h d'un nombre
premier qui divise un coefficient binomial ![]() .
Pour déterminer ce h maximal, on écrit k et n-k en
base p. Le théorème de Kummer dit alors que h est le nombre
de retenues lorsqu'on effectue l'opération k + (n-k) en base p.
Ce qui suit est une version plus courte de l'approche de Mir,
comprenant sa démonstration du théorème de Kummer pour p = 3.
On commence avec une reformulation du problème en terme
d'arithmétique modulaire en base 3:
.
Pour déterminer ce h maximal, on écrit k et n-k en
base p. Le théorème de Kummer dit alors que h est le nombre
de retenues lorsqu'on effectue l'opération k + (n-k) en base p.
Ce qui suit est une version plus courte de l'approche de Mir,
comprenant sa démonstration du théorème de Kummer pour p = 3.
On commence avec une reformulation du problème en terme
d'arithmétique modulaire en base 3:
| 1. | Quand le mot initial est (x0, x1, x2,..., xn),
le mot au bas du triangle est |
Ceci se démontre directement par induction sur n. Comme conséquence immédiate, on a
| 2. | Le résultat est congru à - (x0 + xn) (mod 3) is et seulement
si n est impair et 3 divise |
Notre but est donc de démontrer que la situation décrite en 2 se produit si et seulement si n est une puissance de 3. On note F(n) la plus grande puissance de 3 qui divise n!, c'est à dire que 3F(n) divise n! mais 3F(n) + 1 ne divise pas n!. On a alors
| 3. | F(n) = (# de multiples de 3 <= n) + (# de multiples de 9 <= n) + ... En notation en base 3, Alors Par conséquent, la formule (3) devient , Donc, |
| 4. | Pour étudier la divisibilité de 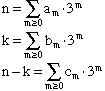
|
| 5. |
Le nombre de fois que 3 divise Selon l'étape (4), ce nombre vaut Soit, après simplification, Nous pouvons maintenant démontrer le théorème de Kummer dans le cas p=3. |
| 6. |
Théorème. La plus haute puissance de 3 qui divise En particulier, on démontre que la dernière somme dans l'étape (5) est le nombre de retenues: Posons em = 1 si il y a une retenue de la m-ième place, et em = 0 autrement (Aussi, e-1 = 0). Alors Donc la plus grande puissance de 3 qui divise 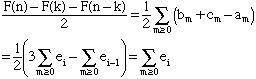
|
Nous sommes enfin en position de retourner au problème initial et démontrer la propriété désirée du triangle de Pascal modulo 3.
| 7. |
Théorème
Démonstration. Le théorème de l'étape (6) nous dit que 3 divise |
Selon l'étape 2, ce théoreme complète notre solution.
Commentaires et notes.
Les théorèmes des étapes (6) et (7) ont été démontrés
dans plusieurs contextes. La meilleure référence au sujet
des résultats de l'histoire de la théorie des nombres est
Dickson [2]. On y retrouve le résultat de Kummer, mais apparemment
Kummer n'a pas interprété ![]() comme le nombre de
retenues. David Singmaster donne l'histoire complète avec plusieurs
références et informations générales. En particulier,
la démonstration des résultats en (5) et (6) ressemble
beaucoup a celle de Mir présentée ici, et on voit
que l'argument de Mir est valable pour tous les nombres premiers,
pas seulement 3.On peut trouver une démonstrastion en francais en [3],
et en espagnol en [4]. On peut aussi démontrer le théorème en (6)
directement, sans utiliser (5). Un argument direct est donné en [1],
mais le lecteur intéressé peut démontrer (6) par induction,
seulement en transcrivant les premières lignes du triangle de
Pascal en notation ternaire et en notant le motif des zéros.
comme le nombre de
retenues. David Singmaster donne l'histoire complète avec plusieurs
références et informations générales. En particulier,
la démonstration des résultats en (5) et (6) ressemble
beaucoup a celle de Mir présentée ici, et on voit
que l'argument de Mir est valable pour tous les nombres premiers,
pas seulement 3.On peut trouver une démonstrastion en francais en [3],
et en espagnol en [4]. On peut aussi démontrer le théorème en (6)
directement, sans utiliser (5). Un argument direct est donné en [1],
mais le lecteur intéressé peut démontrer (6) par induction,
seulement en transcrivant les premières lignes du triangle de
Pascal en notation ternaire et en notant le motif des zéros.
| [1] | Lawrence O. Cannon, Locating multiples of primes in Pascal's Triangle. The College Mathematics Journal 20:4 (Sept. 1989) 324-328. |
| [2] | Leonard Eugene Dickson, History of the Theory of Numbers, Vol. I. Chelsea Publ. 1966. (Originally published in 1919.) |
| [3] | O.M. Fomenko, Sur quelques propriétés des coefficients binomiaux. Mathesis 69 (1960) 291-293. |
| [4] | E. G. -Rodeja F. Una propriedad de los coefficientes binomicos. Rev. Mat. Hisp. -Amer. (4) 24 (1964) 250-253. |
| [5] | David Singmaster, Divisibility of binomial and multinomial coefficients by primes and prime powers. A Collection of Manuscripts Related to the Fibonacci Sequence (18th Anniversary Volume of the Fibonacci Association). pp. 98-113. Fibonacci Assoc., Santa Clara CA. 1980. |