La solution suivante nous a été envoyée par Hua Ma (du département d'informatique à l'Université de Régina), Juan Mir Pieras (d'Espagne) et Midhun Chandran.
Dénotons t l'angle de la région A au sommet A. Les angles dans les régions B et C sont de 30o ± t, tel qu'indiqué dans le diagramme. Soit s, la longueur du côté du triangle équilatéral. Avec l'identité sin 2x = 2 sin x cos x, on obtient les aires des trois régions:
4B = 2s2 sin(30o - t) cos(30o - t) = s2 sin(60o - 2t)
4C = 2s2 sin(30o + t) cos(30o + t) = s2 sin(60o + 2t)
On doit alors montrer que
Puisque sin(60o ± 2t) = sin 60o cos 2t ± sin 2t cos 60o = (sqrt(3)/2)cos 2t ± (1/2)sin 2t,
le terme de gauche est
ce qui est bien égal au terme de droite.
Note: Le rectangle de la figure ressemble à un carré, mais cette apparence est trompeuse. Le rapport de la hauteur AD à la base AB peut varier entre sqrt(3)/2 = 0.866 (lorsque la base du triangle coïncide avec AB) à 2/sqrt(3) = 1.115 (lorsque le côté du triangle coïncide avec AD).
Notre problème provient du journal hollandais Nieuw Tijdschrift voor Wiskunde. Il s'agit du problème 1580 et le journal en a publié lélégante solution géométrique que nous traduisons ci-bas. Elle est due à D. Kruyswijk (Nieuw Tijdschrift voor Wiskunde 55 (1967--1968), page 125). Pour l'apprécier il est essentiel de connaitre les faits suivants au sujet des hexagones réguliers:
- Le côté de l'hexagone détermine un angle de 30 degrés
à partir de n'importe quel point du cercle dans lequel l'hexagone est
inscrit, sauf les points du petit arc déterminé par ce côté.
- Chaque côté de l'hexagone est parallèle à une diagonale, et mesure la moitié de sa longueur.
On veut démontrer que les aires de nos triangles, A, B, et C satisfont à A + B = C. Notons que l'hypoténuse de chacun des triangles est un côté du triangle équilatéral, et ont toutes la même longueur. On glisse une copie de chaque triangle de telle sorte que son hypoténuse coïncide avec le segment EF du côté droit de la figure ci-bas, et que le sommet avec l'angle droit soit sur le demi cercle du haut. Plus précisément, on fait glisser ABP de sorte que A coïncide avec F et P avec E, et de même avec les deux autres triangles. Ensuite on glisse one seconde copie de chaque triangle de façon à placer l'angle droit sur le demi cercle du bas: B correspond à B' et B'', C correspond à C' et C'', et D à D' et D''. Les angles des triangles sont t, t ± 30o et t ± 60o, donc les angles à F qui sont soutenus par deusx sommets successifs sont tous de 30 degrés.
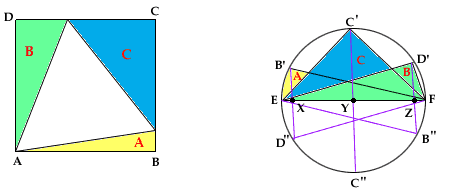
Ainsi, les six points D', C', B', D'', C'', B'' sont les sommets d'un hexagone r\'egulier. Notons X, Y et Z les points où les segments B'D'', C'C'' et D'B'' traversent EF. Alors XD'' = D'Z; de plus, B'D'' et B''D' sont tous deux paralléles à C'C'', et font la moitié de la longueur de ce dernier. On doit démontrer que la somme des aires des triangles EB'F et ED'F donne l'aire du triangle EC'F. Ce résultat découle du fait que ces trois triangles ont la même base, alors que leurs hauteurs respectives sont proportionnelles aux segments parallàles B'X, C'Y et D'Z, où B'X + D'Z = C'Y.