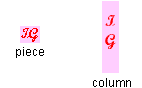| | |
Day 1
Once upon a time, two brilliant scientists, dr. See, and Dr. aitch put their brains together to solve mankind's problems. You will never believe what they discovered After years and years of research they invented a gum which, when chewed regularly, in appropriate quantities, would make people smarter. (I told you that you wouldn't believe it) they decided to call it IntelliGum.
Now, when they marketed IntelliGum they sold it piled in a column. (See the figure below). The number of pieces of IntelliGum in each column depended on the age of the person who was buying it. For example, if a 7 year old bought a column, it must contain 7 pieces of IntelliGum, and if a 20 year old bought a column it must contain 20 pieces of IntelliGum. IntelliGum was also sold in individual packages of one piece, for people who lost some of theirs or who shared some with friends.
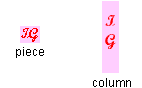
This was such a wonderful idea that people asked to buy supplies of IntelliGum which would last them for a longer time. As a result Dr. see and dr. aitch, the two very brilliant scientists, decided to package their columns in boxes each of which contained as many columns of IntelliGum as the number of pieces in each column. (See the figure below). For example, if each column contained 4 pieces of IntelliGum, then each box would contain 4 columns of gum, and if each column contained 9 pieces of IntelliGum, then each box would contain 9 columns of gum.

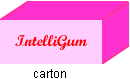
Retailers, who were making a small fortune by selling IntelliGum, put pressure on the good doctors to sell their boxes in larger containers called cartons. (See the figure below). Each carton contained as many boxes as there were columns in a box. So, if there were 9 columns in a box, there would be 9 boxes in a carton, and if there were 12 columns in a box, there would be 12 boxes in a carton.
Soon the wholesalers who were also making lots of loot from the very, very brilliant doctors invention asked for the cartons of IntelliGum to be packed in larger containers called crates. (See the figure below). You can probably guess how they packed the cartons into the crates. That's right there were as many cartons in a crate as there were boxes in a carton. So, if there were 2 boxes in a carton, there would be 2 cartons in a crate, and if there were 17 boxes in a carton, there would be 17 cartons in a crate.

Dr. see and dr. aitch got filthy rich as did the wholesalers and the retailers. Everybody in the world chewed IntelliGum. they solved all the world's problems, and everybody lived happily ever after.
Day 2
Packaging 
Reminder:
- A column of IntelliGum can have any number of pieces of gum in it.
- A box of IntelliGum has as many columns of gum as there are pieces of gum in each column.
- A carton of IntelliGum has as many boxes of gum as there are columns of gum in each box.
- A crate of IntelliGum has as many cartons of gum as there are boxes of gum in each carton.
Use the above information to complete the following table:
| |
Pieces in
a column |
Pieces in
a box |
Pieces in
a carton |
Pieces in
a crate |
| 1 |
2 | | | |
| 2 |
3 | | | |
| 3 |
4 | | | |
| 4 |
5 | | | |
| 5 |
6 | | | |
| 6 |
7 | | | |
| 7 |
8 | | | |
| 8 |
| 81 | | |
| 9 |
| 121 | | |
| 10 |
| 196 | | |
| 11 |
| 225 | | |
| 12 |
| 289 | | |
| 13 |
| | 512 | |
| 14 |
| | 1000 | |
| 15 |
| | 1728 | |
| 16 |
| | 6859 | |
| 17 |
| | 15625 | |
| 18 |
| | | 28561 |
| 19 |
| | | 65536 |
| 20 |
| | | 104976 |
| 21 |
| | | 160000 |
| 22 |
| | | 1500625 |
Day 3
Ordering 
Last day we discovered that if x represents the number of pieces of IntelliGum in a column, then x2 would represent the number of pieces of IntelliGum in a box, x3 would represent the number of pieces of IntelliGum in a carton, and x4 would represent the number of pieces of IntelliGum in a crate. A summary follows:
| Container | Number of
pieces of gum |
| Column | x |
| Box | x2 |
| Carton | x3 |
| Crate | x4 |
When the IntelliGum company shipped an order, they kept track of the number of pieces of gum sent by using an Algebraic expression called polynomial.
An example would be: 8x4 + 4x3 + 7x2 + 9x + 20
- What do you suppose this means?
- When a wholesaler ordered 5 crates, 6 cartons, 8 boxes, 10 columns, and 13 pieces of IntelliGum, how do you think he would represent the total number of pieces of IntelliGum he had ordered?
Workers at the truck-loading platform would receive several orders to be delivered in the same truck. They quickly worked out a way to determine how many of each type of container was necessary. Of course they used algebraic expressions all the time.
- If you were one of the workers and you had to ship the following orders in the same truck, what Algebraic expression could you use to indicate simply, what would be required for the delivery?
Order #1. 8x4 + 7x3 + 9x2 + 8x + 80
Order #2. 2x4 + 3x3 + 6x2 + 5x + 60
- Sometimes retailers would compare information about the number of pieces of IntelliGum they had. Write an algebraic expression to show how many more pieces Order # 1 above has compared to Order # 2.
Interpreting  Orders Orders
- If a retailer was missing 4 cartons in order to have 5 complete crates, what algebraic expression could he use to represent the number of pieces of IntelliGum he has.
- What would a retailer mean if he represented his stock of IntelliGum with the following polynomial? 6x3 - 5x2 + 3x - 1
Adding and Subtracting Polynomials
A. Simplify the following orders
- (2x3 + 5x2 + 4x + 7) + (5x3 + 7x2 + 6x + 14)
- (5x4 + 6x3 + 7x2 + 9x + 5) + (8x3 +2x + 13)
- (x4 + 2x2 + 4x + 1) + (8x3 + 5x2 +7)
- (5x3 - 2x2 + 3) + (2x3 + 4x2 - 1)
- (2x4 - 7x3 + 4x2 - 2x + 9) + (6x4 + 2x3 - 5x2 - 6x - 3)
- (3x4 - 8x3 + 2x2 - 7x + 15) + (2x4 + 5x3 - 4x2 + x - 7) + (9x3 + 6x2 - 8x + 13)
B. Help the retailers compare their stocks of IntelliGum.
- (5x2 + 8x + 6) - (2x2 + 4x + 4)
- (6x3 - 4x2 - 7x + 22) - (5x3 + 7x2 - 4x + 22)
- (5x3 + 6x2 - 3x +12) - (3x3 - 7x2 + x - 9)
- (9x4 + 5x3 + 7x2 + 8x + 24) - (7x4 + 3x3 + 4x2 + 5x + 16)
- (8x4 + 4x3 - 6x2 - 4x + 23) - (2x4 - 6x3 + 5x2 - 4x + 12)
- (7x4 - 5x3 + 6x2 + 8x - 10) - (5x4 - 2x3 - 7x2 + 12x - 15)
Go to Math Central
To return to the previous page use your browser's back button.
|