One of the most interesting and challenging topics of instruction in the middle level mathematics curriculum is the algebra strand. Mention the word "algebra" in your middle years classroom and it is sure to provoke fear and uneasiness. Even the boldest and brassiest early adolescent quivers at the mere mention of the word. Their fear is often a result of hearing older siblings or senior students freely discussing such topics as variables, equations, functions, quadratic transformations, trigonometric ratios, ambiguous triangles and other nebulous ideas.   For several years, I have had the unique opportunity to teach all of the mathematics curriculum from Grade 7 through to Grade 12. This experience has given me an interesting window through which to view the development of mathematical skills over a six year time frame. I have seen the need for concrete and experiential approaches in the middle years and the transition to abstract thinking in very gradual stages.   Is it possible to introduce algebraic concepts to the middle level student without invoking uneasiness and fear? How are we able to develop an algebraic mind set which will lead to successful algebraic abstraction at the secondary level? Unfortunately, the answer does not lie in rigid and formal instructional approaches, nor in drill and more drill. I believe the answer lies in allowing the adolescent mind to explore patterns, to manipulate objects, to discuss with peers the logic of what appears to be happening and to summarize in writing their understanding of an algebraic rule or concept. Our goal in the middle years algebra strand should not be to expect mastery, but rather to encourage a mind set which is curious to explore algebraic patterns and relationships. If we are able to develop this curiosity to explore and analyze patterns then our students will be on their way to acquiring the necessary skills to make algebraic abstractions in later years.   Included in this edition are samples of students' solutions to problems which are based on the discovery and analysis of patterns. These solutions reveal different ways that middle years students understand and analyze problems. Some students are very thorough and creative, others very concrete and some attempt to present their solution in a more formal and abstract manner. Problem Solving Strategies Many of the problem solving strategies outlined in the new middle level curriculum guide encourage the development of algebraic thinking. The following problems, presented as part of the Region 5 curriculum implementation package require the problem solving skills we want our students to have as they learn to analyze patterns and learn about algebraic abstraction. The following strategies are most helpful in solving problems which are algebra or pattern based: Guess and Check Discovering and Extending a Pattern Developing a Table or Chart Using a Diagram Problems to Explore 1. Diagonals in a Polygon In a polygon, a diagonal is a line joining two nonadjacent vertices. A triangle has no diagonals. A quadrilateral has only 2 diagonals. A pentagon has 5 diagonals. Can you discover how many diagonals there would be in a 15 sided polygon? 2. Seven Bags of Marbles Paul places 7 bags of marbles onto a table. The second bag has 2 more marbles than the first bag. The third bag has 4 more marbles than the second bag. The fourth bag has 6 more marbles than the third bag and so on. The total number of marbles in all seven bags is 231. How many marbles are in each of the bags? 3. Squares on a Checkerboard If squares of all possible sizes are taken into account, how many squares are there on an eight by eight checkerboard pattern? 4. A Drink and a Hot Dog At the local hockey rink, the concession has a special on drinks and hot dogs. Kim bought 3 drinks and 2 hot dogs for $6.75. Alana bought 2 drinks and 3 hot dogs for $7.00. What was the cost of 1 drink? What was the cost of 1 hot dog? 5. Red and Black Disks A pattern is made from rows of alternating red and black disks. The first row has only one disk, the second row has 3 disks, the third row has 5 disks and so on. Each row begins and ends with a black disk. How many red disks are there from the first to the fiftieth rows inclusive? 6. Lots of Coins Ryan has been collecting coins for his annual Telemiracle donation. His donation of $7.30 is made up of nickels, dimes and quarters. If he has 47 coins in total, how many of each kind of coin did he have? Is there more than one solution to this problem? 7. Rectangular Catering Services Inc. Sue, the owner of Rectangular Catering Services Inc. is trying to determine the best way of seating customers in her cafeteria. The tables that are used can sit 10 people; four along each side and one at each end. She decides to join the tables together end to end. If her cafeteria has enough length for 10 tables to be placed end to end to make one row, and enough width for 5 of these rows, how many customers could be seated at one time? 8. Walkers and Joggers Beth is a walker who can walk at a pace of 5 km per hour. Lanny is a jogger who runs at a pace of 8 km per hour. Beth is an early riser and Lanny likes to sleep in. On a beautiful spring day, Beth awakens at 7 a.m. and begins her walk. Three hours later, at 10 a.m. Lanny finally awakens and begins to jog, following the same route they always use. Assuming they love to exercise (!), at what time will Lanny catch up to Beth? Plot ordered pairs of (time, distance) on the coordinate plane to illustrate Beth's and Lanny's journeys. The Problem: Squares on a Checkerboard If squares of all possible sizes are taken into account, how many squares are there in an eight by eight checkerboard pattern? Lacey's response to the checkerboard problem: To find out how many squares there are in an eight by eight checkerboard I multiplied 8 by 8 to find out how many small squares there are (see the following diagram). There are 64 small squares. I continued to find out how many squares there are that consist of 4 small squares (see the x's). I counted the squares on the bottom of the checkerboard. There are 7 on the bottom which means there are 7 on the side. To find out how many squares there are I multiplied 7 by 7. I got 49. Now I counted how many squares there are that are made up of 9 small squares (see the O's). Once again I counted how many there were on the bottom and the side. There were 6 on the bottom and 6 on the side. I multiplied 6 by 6 and got an answer of 36. Next I needed to know how many squares there are that have 16 smaller squares in them, I discovered that there were 5 on the bottom and 5 on the side. I multiplied 5 by 5 to get an answer of 25. I then wanted to know how many large squares there are that are made up of 25 small squares. I found out there were 4 on the bottom and that means there are 4 on the side. I multiplied 4 by 4 to get an answer of 16. I needed to find out how many squares there are that are made up of 36 small squares. There were 3 on the top and 3 on the side, 3 x 3 is 9, so there are 9 squares like that. To find out how many bigger squares there are that consist of 49 small squares I once again counted how many bigger squares there are on the bottom and side and multiplied this number. There are 2 on the top and bottom which means there are 4 in total. (2 x 2 is 4) Now I added together all the answers: 64 + 49 + 36 + 25 + 16 + 9 + 4 + 1. I added on the 1 because you can not forget the actual square that runs along the outside of the checkerboard. This makes a total of 204 squares of all different sizes. 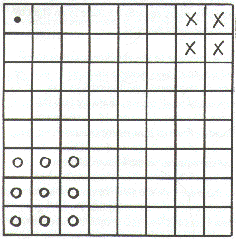Lacey Walker, Grade 6, Star City School The Problem:A Drink and a Hot Dog At the local hockey rink, the concession has a special on drinks and hot dogs. Kim bought 3 drinks and 2 hot dogs for $6.75. Alana bought 2 drinks and 3 hot dogs for $7.00. What was the cost of 1 drink? What was the cost of 1 hot dog? Kendra's response to the drink and hot dog problem: I did this question by using the guess and check method. I kept trying different prices until I got it to match the first clue. Then I tried the numbers to see if they would work in the second clue. When my prices worked in both clues then I knew they would be my answers. I made a chart to show how this works. 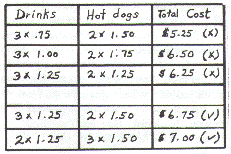(See diagram below.) Kendra Rislund, Grade 8, Star City School Kyle's response to the drink and hot dog problem: If this question was put into an algebraic expression it would be written as: 3d + 2h + 25 = 2d + 3h Then I could work with this equation like this: 3d + 2h + 25 = 2d + 3h 3d + 2h = 2d + 3h - 25 1d + 2h =     3h - 25 1d =     1h - 25 From the last statement I know that 1 drink costs 25 cents less than 1 hot dog. Then I did guess and check using prices that were 25 cents apart. I found that when a drink costs $1.25 and a hot dogs costs $1.50 my algebraic expression works: 3($1.25) + 2($1.50) + ($0.25) = 2($1.25) + 3($1.50) $3.75 + $3.00 + $0.25 = $2.50 + $4.50 $7.00 = $7.00 Kyle Penner, Grade 8, Star City School Return to Math Central To return to the previous page use your browser's back button.