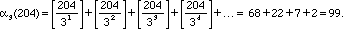
A recent question and answer sent to Quandaries and Queries was
"Are there infinitely many n such that 105 "divides" 2n choose n?
Erdos, Graham, Rusza and Straus (Math. of Comp., 29(1975),pp 83-92) show that for any two primes p and q there exist infinitely many integers n for which (C(2n,n),pq) = 1. They remark that nothing is known for three primes and, in particular, they ask whether there are infinitely many n for which (C(2n,n),105) = 1 and this is your problem. As far as I know this is still unsettled.
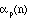 is the power to which p divides n! then
is the power to which p divides n! then
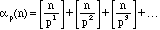 where the square brackets [] denote the greatest integer function. For
example, the largest power of 3 in 204! is
where the square brackets [] denote the greatest integer function. For
example, the largest power of 3 in 204! is
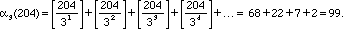
This is because 3 divides every 3rd number in the sequence 1, 2, 3, ... , 204; 32 divides every 9th number in the sequence 1, 2, 3 , ... , 204; and 33 divides every 27th number in the sequence 1, 2, 3, ... , 204; and 34 divides every 81st number in the sequence 1, 2, 3, ... , 204.
Similarly if you wanted to find out how many zeroes appear at the end of 204! what you really need to find out is how often 5 divides 204! That's
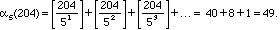
Note that if we write 204 in base 3 (see
Converting to other bases in Quandaries & Queries), i.e. 204
= 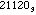 the sum of the digits in base 3 is 6. If we write 204 in base 5 we get 204 =
the sum of the digits in base 3 is 6. If we write 204 in base 5 we get 204 =
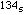 the sum of the digits is 8. Observe that (204 - 6 )/(3 - 1) = 99. Observe
also that
the sum of the digits is 8. Observe that (204 - 6 )/(3 - 1) = 99. Observe
also that
(204 - 8 )/(5 - 1) = 49. Is this an accident, getting 99 and 49 again this way? It isn't. The proof is a little messy but not too hard, however we won't go through it here. Let's have a peek at what goes on though.
Let me write Sp(n) for the sum of the digits of n in base p. We can in
general show that the power to which p divides n! can be expressed as
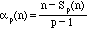 .
The interested reader might then want to see how often a prime p divides
.
The interested reader might then want to see how often a prime p divides
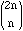 ,
as was asked in the Quandaries and Queries question, call it
,
as was asked in the Quandaries and Queries question, call it
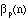 ;
we find, looking at the factorials in the numerator and denominator of
;
we find, looking at the factorials in the numerator and denominator of
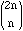 that
that
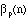 =
=
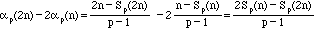 .
.
For example, 204 =
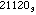 and 102 =
and 102 =
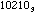 . Thus
. Thus
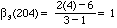 .
Similarly 204 =
.
Similarly 204 =
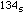 ,
102 =
,
102 =
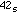 thus
thus
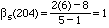 . That is both 3 and 5 divide 204 choose
102 to the first power only.
. That is both 3 and 5 divide 204 choose
102 to the first power only.
To return to the previous page use your browser's back button.