1. Get the students involved in a problem where they go through the different stages of the problem-solving process (in groups), with the teacher directing the problem solving inquiry.

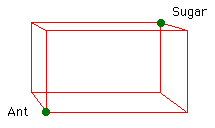
An example is the ant and sugar problem. An ant is at one corner of a box and wants to get to a sugar cube is at the diagonally opposite corner.

Each group of students should pay attention to its particular group strategy used and try to identify it from the list of strategies. Each group should try to identify the process it went through either as a group or individually within the group as it came up with possible strategies to solve the problem. Each group of students should discuss the problem and come to an understanding of what it is asking for; conferencing about the problem can assist the students in clarifying their expressed ideas. The teacher can help the group to understand the problem by asking questions which open up the conversation and by asking the students to convince others and to justify their strategy. The students should make a record of their solution process, including all their `rough work.' They can then present their finished product/process to the class. If teachers do one problem like this in depth each week they will enable their students to explore many different strategies. As new strategies emerge in the solving of the problem, the teacher can label them. As the teacher addresses the different problem solving stages, those stages shgould also be labelled. We should teach problem solving (process and heuristics) from within a problem.

2. In addition to doing one major problem a week in depth (as in # 1), we should also be providing children with a `problem-of-the-day.' This problem could be on the board when the children come into class in the morning, and, at some point during the day, it can be worked on by children individually, or in groups, and then later in the day it can be worked on as a whole-class activity. The purpose of this problem can be to focus on a specific mathematical concept, practice a skill area or a problem heuristic, etc. This problem can, of course, be used by the teacher to introduce the mathematics concept to be studied that day.

3. Encourage children to bring in their own puzzles or problems and/or create or compose them together in class. Have a problem-creation station.

4. Post the Polya problem solving plan and a list of heuristics (with icons) -- make it clear that these are only guides.

5. Model problem solving -- do it yourself and make sure the children see you struggling with some problems. You must be seen to be convinced of what you advocate.

6. Within the school promote mathematical problem solving in the form of formal programs such as "Math Olympics," or "Odessay of the Mind," or simply begin a math club which meets weekly to do math problems -- i.e., everyone does them, teachers and students. Someone brings a problem to the club, or continues to work on one from before, and everyone works on this problem together (in groups). Problems are recorded when they are submitted to the group; the name of the submitter and/or the creator is recorded; the length of time spent on this problem, and the different strategies tried are recorded; finally the solution and the names of person(s) solving the problem are recorded. This provides a problem log. During the course of a semester only four problems may be completed.

7. Keep records of the problems in # 6, but also keep watchful for interesting problems in books, newspapers, magazines, etc. Collect and organize these problems for children to work on.

Bibliography

Burton, L. (1984). Thinking Things Through. Problem Solving in Mathematics. Oxford: Basil Blackwell.