Diamond Slopes and Speedy Whales via… One Identity

One Identity.$^1$ Show that  $\tan^{-1} x + \tan^{-1} y = 2 \tan^{-1} \Large{\frac{s}{p + \sqrt{s^2 + p^2}}},$
where $s = x + y, p = 1 - xy.$

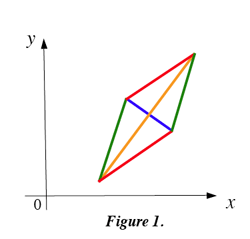Diamond Slopes If $m$ is the slope of rhombus diagonal drawn in the Cartesian plane (see Figure 1), and $l, n$ are the slopes of its sides, then \[m = \frac{a}{b \pm \sqrt{a^2 + b^2}},\] where $a = l + n, b = 1 - nl.$ Prove it. Hint. You may use One Identity.

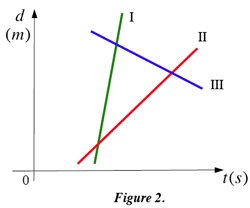A Three-Speedy-Whales Problem.$^2$ auf Deutsch en français  Once upon a time three whales were swimming along the north-south shoreline in the ocean near the island. Children at the island lighthouse observed whales’ motion and drew their position-time graphs in Cartesian coordinates. They noticed that intersections of three graphs form an isosceles triangle (see Figure 2). If the first whale swam at 7 m/s [N] and the second one at 1 m/s [N], what is the velocity of the third whale? Hint. You may use Diamond Slopes Rule.

Solve Equation: $2 - 2x - 2x^2 = x \sqrt{5 + 5 x^2}$.   
                              Hint. Use One Identity to get  $3 \tan^{-1} x = \tan^{-1} 2.$

          ______________________

$^1$ first appeared in 1999 volume 2 of Matematyka v Shkoli, the journal of the Ministry of Education and Science of Ukraine

$^2$ first appeared in 2010 volume 48:1 of delta-k, the journal of the Mathematic Council of the Alberta Teachers' Association

Copyright © March, 2010 by Gregory V. Akulov, Oleksii V. Akulov