GRADE 7

UNIT: Math: Shape and Space; Science: Force and Motion
THEME: Human Face of Mathematics - Mathematics in Aboriginal Culture

• EQUIPMENT
• atlatl and dart
• pylon (or other easily seen target that cannot damage or be damaged by the dart)
• measuring tape
• coloured tape
• Coordinate plane

LEARNING OUTCOMES:
Math - Shape and Space

SS7.4 Demonstrate an understanding of the Cartesian plane and ordered pairs with integral coordinates.
SP7.1 Demonstrate an understanding of the measures of central tendency and range for sets of data.
SP7.3 Demonstrate an understanding of theoretical and experimental probabilities for two independent events where the combined sample space has 36 or fewer elements.

Science - Force and Motion

• Recognize the relationship between force and motion.
• Describe and analyze motion.
• Identify which factors that influence motion are forces or related to forces.
• Know the forces which influence various types of motion.
• Design experiments to demonstrate the relationship between force and motion.
  

Introductory Activity modified from Poverty Point Expeditions, by Debbie Buco, Louisiana Division of Archaeology, Activity Booklets

Choose 3 students to simulate the rotation of the hand and the atlatl around the shoulder joint. One person will pretend to be the hand and observe how fast the spear would travel if the hand threw it. Another group member will pretend to be the atlatl and observe how fast the spear would travel if the atlatl threw it.

Measure and cut a piece of string or rope which is four feet long. Place a mark in the middle of the string, two feet from both ends. The "shoulder joint" member will kneel down while holding the tip of the string stationary on top of their head. The "hand" person will hold the string securely at the two foot measurement, and the "atlatl" person will hold the end of the string (four feet from the "shoulder joint" person.)

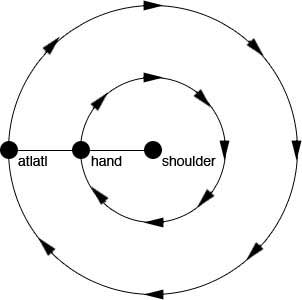
The "atlatl" person must keep the string taut at all times while walking in a circle around the "shoulder joint" person. The "hand" person must keep pace with the "atlatl" person. Have the class determine who is running faster.

This demonstrates how throwing with an atlatl increases the speed of the dart as it is thrown. A dart which is thrown from an atlatl the length of your arm would travel approximately twice as fast as a dart thrown by the hand. For an even more vivid simulation, increase the length of the radius for the atlatl to about six feet. The larger the radius, the faster the "atlatl" will travel.

Teacher Set Up

1. Create an x & y axis from coloured tape, each measuring 10 m.
2. Starting from the origin, in each direction, mark the tape in increments of 25 cm.
3. Create a circle of radius 3m, centred at the origin.
4. Place the pylon at the origin
5. Divide the class into groups of no less than 3. For each group you will need one student to throw the dart, one student to measure distance and another to plot the data. One student from each group will throw the dart for the sake of consistency.

Student Instructions
Average Distance from the Target

1. Starting from -10m on the y axis, throw the dart a minimum of 20 times, aiming at the pylon. Plot where the atlatl lands compared to an origin, x & y axis (ignoring any that fall outside the axes).
2. From plotted data, determine the average distance from the origin for each “good” throw.
3. Determine the experimental probability that a throw will be within 3 metres of the origin.

Motion of the Atlatl and Dart

1. While the dart is being thrown, observe the thrower from the side.
2. Through the course of all of the trials, describe and sketch the motion of the thrower and the path of dart for the farthest and most accurate throws. (Bare in mind that the farthest throws may not be the most accurate).
3. Investigate why this motion is the optimal.

Lessons for Atlatl Users with Some Experience - Grade 7 PDF

Atlatl Home Page