represents and offers some activities that will enable them to arrive at their own approximations of within bounded limits.
To use the methods that follow, your students will need to know the basic trigonometric ratios. They will also need to use the trigonometric function keys on a calculator. By building on these skills, the activities might provide a good preparation for the the idea of limits in a pre-calculus context. An optional activity requires a computer with a fairly basic spreadsheet application.
The motivation for this article comes out of some responses to the question 'what is
?'. Some students seem to think it is merely a number which is used to calculate the area of a circle or its circumference. One mature-age student had been told in the pre-calculator days that was 22/7, and that was that! Often, seems to be 'defined' as a calculator key. Not often enough, perhaps, is seen for what it is: the exact ratio of the circumference (C) of a circle to its diameter (d).
At all events, it doesn't seem to be widely recognised that
is an extremely important number which has many interesting properties and is deserving of study in its own right.
Adapting Archimedes
I believe a good way to get an 'intuitive feel' for the fact that = C/d is by following the reasoning used by Archimedes who developed the first scientific method for calculating in about 240BC. [You may wish students to construct some or all of the following diagrams with a compass and protractor or you may prefer to use prepared overhead transparencies.]
Archimedes' reasoning went roughly like this:
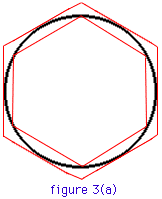
| if you take a circle and circumscribe it with hexagon, then the perimeter of the hexagon will be longer than the circumference of the interior circle - figure 1(a) | |
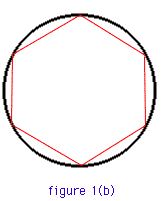
| if you were to take the same circle and inscribe a hexagon within it, then the perimeter will be less than the circumference in length - figure 1(b) |
 |
 |
 |
 |
 |
 |
The bottom line is that by expressing the perimeters of the 96-sided polygons to the diameter of the circle, he knew that:
< 22/7.
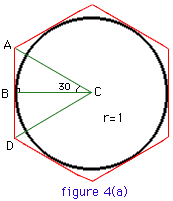
We start by calculating the lengths of one side of a polygon. Students should begin by constructing two circles of the same arbitrary radius which can be set to r = 1. By using a protractor, hexagons can be readily constructed in the following fashion - figures 4(a) and (b).
 |
 |
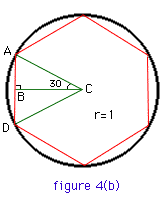| tan(60/2) = tan(30) = AB / 1 | |
 | AB = tan(60/2) |
| perimeter of circumscribed polygon = 2 x 6 x tan(60/2) |
| = C/d < 12 tan(60/2)/2 |
| < 3(2) tan(60/2). |
| sin(60/2) = sin(30) = AB / 1 | |
| AB = sin(60/2) |
| perimeter of inscribed polygon = 2 x 6 x sin(60/2) |
| = C/d > 12 sin(60/2)/2 |
| > 3(2) sin(60/2). |
< 3(2) tan(60/2).
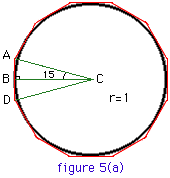
Now we want to double the number of sides to the polygons so that we get a better approximation of the circumference. Students should quickly grasp that this is done by bisecting the angle ACB in each case - figures 5(a) and (b).
 |
 |
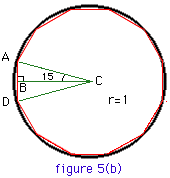For example for the circumscribed polygon - figure 5(a)
| tan(60/4) = tan(15) = AB / 1 | |
| AB = tan(60/4) |
| perimeter of circumscribed polygon = 2 x 12 x tan(60/4) |
| = C/d < 12 tan(60/4)/2 |
| < 3(2x2) tan(60/(2x2)). |
Sequences
By now it may have occurred to some students, at least those who have some knowledge of sequences and series, that two sequences emerge from the continuous doubling of the number of the sides and the bisection of the angles. The number of sides of the polygons are
6 = 3(2), 12 = 3(2x2), 24 = 3(2x2x2), 48 = 3(2x2x2x2),...
and the angles are
30 = 60/2, 15 = 60/(2x2), 7.5 = 60/(2x2x2), 3.75 = 60/(2x2x2x2),...
Thus, we can state that
--- (*)
With this limit-bounded formula, students could of course play around with their calculators to get various approximations of . If your class has access to a standard spreadsheet, you may wish to try the following activity.
Using Computers
It is simple enough to use a standard spreadsheet to get a table of successive approximations of .
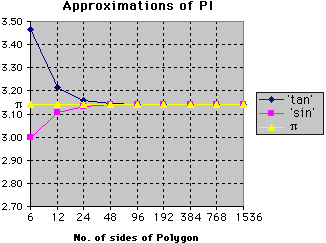
| No. Sides | n |  | Rel. Error |  | Rel. Error | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 1 | 3.464102 | 10.265779 | 3.000000 | -4.507034 | |||||
| 12 | 2 | 3.215390 | 2.349052 | 3.105829 | -1.138407 | |||||
| 24 | 3 | 3.159660 | 0.575100 | 3.132629 | -0.285334 | |||||
| 48 | 4 | 3.146086 | 0.143035 | 3.139350 | -0.071379 | |||||
| 96 | 5 | 3.142715 | 0.035713 | 3.141032 | -0.017848 | |||||
| 192 | 6 | 3.141873 | 0.008925 | 3.141452 | -0.004462 | |||||
| 384 | 7 | 3.141663 | 0.002231 | 3.141558 | -0.001116 | |||||
| 768 | 8 | 3.141610 | 0.000558 | 3.141584 | -0.000279 | |||||
| 1536 | 9 | 3.141597 | 0.000139 | 3.141590 | -0.000070 |
At this point, students could reflect on:
which side of the limit, 'tan' or 'sin' boundaries, starts-off as a better approximation to
the rates at which they appear to converge towards
Archimede's limit for the 96-sided polygon given above.
Plotting the data might assist:
Conclusion
The purpose of this article was to heighten students' appreciation of as an irrational number by first demonstrating that the circumference of a circle can be approximated by considering the inscription and circumscription of a series of polygons. Students will then see that by expressing these approximations as a ratio to a diameter, exists within bounded limits and hence can be approximated as accuracately as we please (as Archimedes himself might have said).
The history of is quite fascinating and covers a wide range of mathematical concepts. There is a lighter side to its history as well which can be used to good effect in the classroom.
Note:
Students learning calculus might find the inequatities (*) interesting in another situation. Dividing through the inequalities (*) by
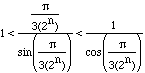
Hence, as n increases, 
approaches 0 and hence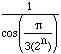 
approaches 1.
Thus
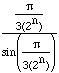is sandwiched between 1 and a sequence that converges to 1, giving some justification to the fact that
References
| Eves H (1990) | An Introduction to the History of Mathematics Orlando, FL: Sanders College |
| Heath T (1963) | Greek Mathematics New York: Dover |
| Katz VJ (1993) | A History of Mathematics: An Introduction New York: Harper Collins |
