A Rise over Run, and a 10 versus 1

The slopes of parallel and perpendicular lines, $m_{\parallel} = m$ and $m_{\perp} = -m^{-1}$ belong to basics of Cartesian geometry. Students discover them in grade 10, examining the lines positioned specifically at two angles $0$ and $\pi/2.$ For the rest of their high school years, students’ notion of slope relationships remains at this junior level.  Considering that it is way more likely for the slope relationship to involve angles other than $0$ and $\pi/2,$ grade 11-12 students could discover more general approaches that are practical for various angles.  

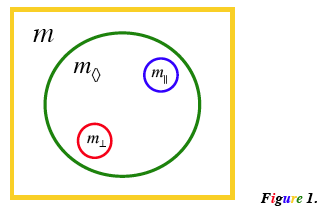
Although the expressions for $m_{\parallel}$ and $m_{\perp}$ look different, there are some fundamental attributes common to both.  Both are primary, symmetric, and both are the slopes of the angle bisector, or diamond slope(s), denoted further $m_{\large \diamond}$ (Figure 1).

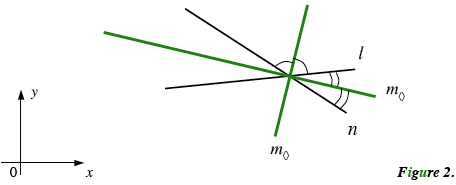
     For lines, with slopes $l$ and $n$ (Figure 2), $m_{\large \diamond}$ can be written as follows¹

\[ \frac{a}{b \pm \sqrt{a^2 + b^2}},\]

where $ a = l + n,  b = 1 - ln.$

Let the acute angle between these lines approach zero, and the obtuse angle approach $\pi.$ This leads to the case with two equal slopes, say $m$ (Figure 3).

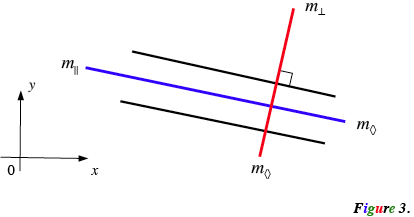
Angle bisector of the angle zero becomes a parallel line, and angle bisector of the straight angle becomes a perpendicular line. Algebraically it implies:

$$ \small m_{\large \diamond}
= \small \frac{m + m}{1 - m^2 \pm \sqrt{4m^2 + \left(1 - m^2 \right)^2}}
= \small \frac{2m}{1 - m^2 \pm \left(1 + m^2\right)}=
\small \left\{ \begin{array}{ll} m_{\normalsize \parallel} & \mbox{ for "}+\mbox{"} \\ m_{\normalsize \perp} & \mbox{ for "}-\mbox{"} \end{array} \right. $$

and the slope relationships for parallel and perpendicular lines are formally deduced as a corollary of $m_{\large \diamond}.$ Combined together, $m_{\parallel}$ and $m_{\perp}$ solve only one special case of diamond slopes.

   In the table below are comparative examples involving some of the most frequent symmetric shapes on the plane. The first column represents the set of exercises, where the goal is to find the slopes of “dotted” sides, provided that slopes of “solid” sides are given. Such models often appear in applied contexts. The second column shows (in green) to what extent particular exercise can be solved using $m_{\large \diamond},$ and third column shows (in blue and red) to what extent the same exercise can be solved using $m_{\parallel}$ and $m_{\perp}$ alone. “Overalls”, the last row of the table, vary from one set of examples to another, but not significantly, provided that fair variety of shapes is included.

Triangles: right isosceles (1), isosceles (2, 3)

Quadrilaterals:
square (4) , rectangle (5), rhombus (6) , deltoid (7), and isosceles trapezoid (8)

Regular polygons: pentagon (9),  octagon (10)

   Our informal comparison, rounded to “ten versus one”, indicates that $m_{\large \diamond}$ could significantly strengthen $m_{\parallel}$ and $m_{\perp}$ over the course of high school Mathematics. As a concept, the slope of the angle bisector establishes cognitively demanded connection/generalization of $m_{\parallel}$ and $m_{\perp}.$ The trio $m_{\parallel}, m_{\perp} \mbox{ and } m_{\large \diamond}$ accompanies teaching for deeper understanding, develops incomparably larger array of solvable applied problems, renewing and moving learning outcomes forward.

Copyright © April, 2011 by Gregory V. Akulov