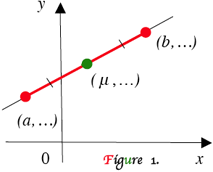
The well-known midpoint formula tells that, if the straight line’s segment has the ends at $x = a, b,$ and midpoint at $x = \mu$, then $2 \mu = a + b \mbox{ or } \mu = \large \frac{a + b}{2}.$ It also tells that the same relationship holds for y-values. Circular analogue of midpoint formula is a new topic.
|
 |
Arc Midpoint Computation
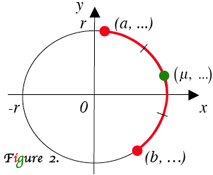
Let origin-centered arc of radius $r$ (see Figure 2) have the ends at $x = a, b,$ and midpoint at $x = \mu.$ Then
\[2 \small \mu = \pm \sqrt{(r + a)(r + b)} \pm \sqrt{(r - a)(r - b)}\; , \]
where the first radical gets “−” iff1 the arc has a negative x-intercept, and
the second radical gets “+” iff the arc has a positive x-intercept.
The same relationship holds for y-values.
Examples
A . Origin-centered arc of radius 50, located as shown at Figure 2, has the ends at $x = 14$ and $x = 25$. Find x-coordinate of its midpoint.
B . An arc of radius 40 is centered at origin. It starts and ends a $x = \;‒24$ and $x = 9$. What is x-coordinate of arc’s midpoint, if the arc is located in quadrants I and II?
C . An arc has center at $(0, 0)$ and radius 82. It starts at $y = 18$ in quadrant II, passes through quadrants III and ends in quadrant IV at $y = \;‒1$. What is y-value of arc’s midpoint? |
 |
Solutions
A . $r = 50, a = 14, b = 25,$ both radicals go with “+”, and $20 \sqrt{3} + 15$ is the answer;
B . $r = 40, a = ‒24, b = 9,$ first radical goes with “+”, second radical goes with “−”, and $14 - 4 \sqrt{31}$ is the answer;
C . $r = 82, a = 18, b = \;‒1,$ both radicals go with “−”, and $-45 - 4 \sqrt{83}$ is the answer.
Arc midpoint computation was suggested by first attempt shown in [1]. Details of proof involved identities received from [2].
References
- Oleksandr (Alex) G. Akulov (2009). Dot product finds arc midpoint. Math News, U of W. Volume 111, Issue 6, p. 5.
- Gregory V. Akulov (2010). The slope of the angle bisector relationship in applied and theoretical problems. Vinculum, SMTS. Volume 2, Number 1, p. 49.
______________________
1The word iff first appeared in 1950s as a shortening of conjunction if and only if.
Copyright © January, 2011 by Gregory V. Akulov, Oleksandr (Alex) G. Akulov
In May 2016 Oleksandr and Gregory sent us
an Arc Midpoint Calculator.
Arc Midpoint Calculator 1
Oleksandr G. Akulov,
MM in OR, BMath, Vancouver, British Columbia
Gregory V. Akulov, teacher, Luther College
High School, Regina, Saskatchewan
Copyright © May 19, 2016 by
Oleksandr G. Akulov, Gregory V. Akulov
|

