Within the broad concept of farming, there are two very important elements: time and money.  At the root of both of these is mathematics.  Mathematics has enabled farming to be more economically efficient and has increased productivity.  Farmers use mathematics as a system of organization to effectively utilize their time and manage their money.  Farmers use numbers everyday for a variety of tasks, from measuring and weighing, to land marking.  I intend to explore some of the ways math is used in farming.

Obviously, numbers are an integral part of farming.  Locations and machines are commonly described or labeled with numbers.  More importantly, however, is what these numbers mean.  The numbers are not arbitrarily assigned; they have a purpose.  Consider land locations.  A sample land location, where I live in Saskatchewan, Canada, is  SE 32 – 15 – 8 – W3.  These numbers mean that this particular piece of land is located in the southeast quarter of section 32, township 15, range 8, west of the 3^rd meridian.  The province of Saskatchewan is divided into 36 sections within a township.  Further, each section is separated into four quarters.  In this way, rural Saskatchewan can find specific land locations based on numerical directions.  This is a recognized mathematical system. 

One of the most frequently used math concepts on the farm is the use of proportions.  Units and measurements used in farming are fairly unfamiliar to other areas.  We can use proportions to make conversions from the unfamiliar to the familiar.  Land is measured in acres, for example.  It is hard to understand the size of an acre because our minds are trained to visualize miles or kilometers.  We can use conversions to put an acre into perspective.  There are 43,560 square feet in an acre.  This is slightly smaller than the size of a Canadian football field, without the end zones.  Other farm measurement terminology include quarters and sections.  A quarter is 160 acres and a section is 4 quarters.  Professionals who work in grain elevators frequently use conversions.  Grain prices are often given per ton, but producers want to know the price per bushel.  Agriculture specialists are required to do these conversions quickly and accurately.

The agriculture community uses numbers to describe and grade seeds.  Weights of seeds are generally expressed in terms of bushels.  For example, wheat is maybe 60 lbs/bu and perhaps barley is 48 lbs/bu.  Seeds are graded using numbers as well.  For example, spring wheat can be given a grade of 1, 2, 3, 4, or feed.  Durum can be given a grade of 1, 2, 3, 4, 5, or feed.  Barley can only be given a grade of 1, 2, or feed.  Peas are either edibles or feed.  In order for peas to be edible, they need a grade of 2 or better.  In the case of durum, an HVK (hard vitreous kernels) measurement is one of the determining factors of a grade.  HVK is a percentage measurement of hardness, which is examined by natural translucency, in a 25g sample.  For a number one durum, the seeds need to have 80% HVK, for a number two durum, the seeds need to have 60% HVK, and so on.  Elevators have a special scale that gives a measurement of HVK percentage.  All of these number systems are used to categorize seeds.  Theses numbers are determinants for grain pricing and are extremely valuable for producers and consumers.

Part of a ripe barley field near Morse, Saskatchewan, Canada.

Estimation is an important concept for farmers.  Much of farming is unpredictable, due to weather reliance and grain markets.  Farmers try to estimate the yield of a certain field of grain.  To do this, farmers pick a plant and count how many seeds are on the head.  By looking at the square footage of a field and estimating the number of heads, farmers can find an approximation of the yield.  It can be very difficult to estimate crop yields and sometimes, professional estimates are very inaccurate.

The head of a barley plant from the field pictured above.

Farmers will also estimate elements of time.  They know approximately how many hours they will need to seed and harvest and can plan accordingly.  These estimates of time are based on crop types and machine availability, as well as human resources.  Farmers consider past trends of weather and moisture conditions to decide when to start seeding.  Furthermore, farmers can estimate the time remaining until harvest by calculating growing degree days.  This is the measurement of heat units needed by the plant to reach its full maturity.  It also accounts for the ripening of the crop.  An approximation is made of how many days remain until the crop is ready to be harvested.  Some processes affect this calculation such as desiccating the crop, and can change the number of growing degree days.

A combine after harvesting a field of barley.

Farmers need to consider all aspects of their farming operation in order to make it successful.  Farmers create mathematical systems of equations and inequalities to help them make decisions about which crops to plant in which fields.  This system of organization is commonly referred to as linear programming.  The constraints of farming can include costs of seed, labour, time, crop insurance, machinery, chemical / fertilizer, and so on.   Livestock producers also use linear programming when making feed for cattle.  A variety of ingredients are mixed together to make feed and producers want the most nutritious combination of ingredients that is also cost efficient.  There are also formulas that illustrate the relationships between relative humidity, time, and moisture content that are used by farmers to estimate drying time before baling alfalfa.

The following problem illustrates how a young livestock farmer may use linear equations, linear inequalities, and mathematical organization:

Maurice, who is 14, lives on a farm and wants to earn some money for a snowboard this fall. It costs $450.  He talks to his parents and decides he will raise some free-range chickens to sell.  His parents agree to lend him the money to do this if he pays them back when the chickens are sold.

He makes a list of his costs and his time requirements:

1.    He needs to prepare a warm, dry shelter for the chicks.  He will need chick starter (special food) that costs $1 per chick.  It will take 2 hours of his time. 

2.          His mom will give him a ride to the hatchery where he can buy the chicks for $1.20 each.  Maurice has to pay $12 for gas and it takes him 2 hours to collect the chicks.

3.          For the next sixteen weeks, the chicks grow into adulthood.  Once they are finished the chick starter formula, they eat grass, which costs him nothing.  Maurice expects to lose 10% of his birds before they are fully grown.  He has to spend 5 hours per week doing chores like providing fresh water, checking on them, cleaning their roosts, etc.

4.          Maurice is a bit squeamish, and he decides that he'll take the fully-grown chickens to a commercial processor for killing and cleaning. His father has a truck that will be able to carry the chickens to the slaughterhouse, but it will cost $20 in fuel and take 4 hours of Maurice's time.  The processor charges $3 per bird for its services. 

5.          When he gets the chickens home, Maurice has to weigh, bag and freeze them.  That takes an average of 5 minutes per bird. He estimates the average weight will be 5.5 pounds.  Fortunately, his mother is letting him use her extra freezer for free. 

6.          He decides that he can charge $3.00 per pound if his customers pick up their orders (he won't be doing any deliveries). 

Question 1: How many chickens does he need to order so that he can raise the money for the snowboard, keeping in mind that Maurice needs to repay his parents for the money he borrowed from them? 

Question 2: If Maurice purchases that many chickens, what would his hourly wage be if he made $450?

Solution

Question 1: Make a chart recording the expenses, revenue, and labour values from the problem.  We can define variables for c (the number of chickens bought) and c¢ (the number of chickens that survived the 16 weeks).

	Expenses (in dollars)	Revenue (in dollars)	Labour (in hours)
1.	1c		2
2.	1.20c + 12		2
3.	c¢ = 0.9c		80
4.	3c¢ + 20		4
5.		16.5c¢	1/12 c¢

Maurice’s total profit is his revenue minus his expenses.  We can sum up his expenses as follows:

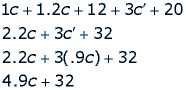
Then, Maurice’s profit would be:

Maurice’s profit needs to be at least $450 if he wants to purchase the snowboard.  We can set up an inequality to find the minimum number of chickens that must be purchased for Maurice to afford the snowboard.

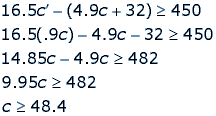
Maurice needs to purchase at least 49 chicks in order to afford the snowboard once he sells the chickens, fully grown.

Question 2:  We can use information from the chart above to find the total number of hours Maurice worked.

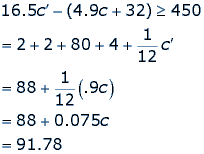
Total time in hours = 91.78

If Maurice works a total of 91.78 hours and makes $450, his hourly wage can be found simply by dividing.

If Maurice got paid an hourly wage it would be $4.91 an hour.  Farmers use this same sort of mathematical organization, although more complicated, to make decisions about their farm that will provide optimal profits.

Farmers use math when applying chemicals and fertilizers to crops.  A farmer may want to spray 160 acres at .8 L/hectare and needs to know how much chemical he should purchase.  Different chemicals are applied at different rates for different crops at different times during the growing season.  Conversions also need to be made for hectares and acres.  Some chemical application rates will be given as .5 to 16 oz/acre or in L/hectare, as in the example above.  When working with fertilizers, farmers must determine how much of a particular nutrient is needed for a specific crop, and apply the fertilizer accordingly. 

A fertilizer bin located on a farm south of Morse, Saskatchewan, Canada.

The following formula is an example of a calculation that is used by farmers and custom spray specialists to find the number of gallons per acre needed to spray a certain section of land.

gallons per acre =	5 940 · gallons per minute (per spray nozzle)
	miles per hour · nozzle spacing (in inches)

Geometry is a crucial skill for farmers when spraying.  The booms on a high clearance sprayer span 90 feet.  If a farmer needs 200 acres of a field sprayed, he can estimate how many passes the sprayer will need to take in order to cover the field.  This will require conversions of acres to feet as well as some geometric organization.  Because the crops in the field may have come up already, farmers want the fields sprayed effectively with the least number of passes.  Chemicals are purchased in concentrate and need to be diluted with water.  Most chemical companies will provide instructions for the amounts to be mixed.  When custom spray specialists are instructed to spray a section of a field, say 200 acres, they need to determine how much chemical they will need, how much and how often they will need water (based on the application rate), and how long the job will take (dependant on the size of the sprayer and rate of application).  Different rates can drastically alter time requirements.

A water tank used to haul water for spraying purposes.

At the conclusion of harvest, farmers need to decide if they have enough storage for their seeds.  Farmers use formulas to determine how many bushels a bin will hold.  This can be determined by finding the volume of the bin (in cubic feet) and converting the measurement to bushels, since 1 bushel is 1.244 cubic feet.  Farmers may also want to determine the volume of stored grain already in the bin.  To do this, they use a formula, such as the one illustrated below (all measurements in feet):

Bushels in the bin = 0.8036 (length) (width) (average depth of grain)

This will give the farmer an estimate of how many bushels of a particular grain are in a rectangular bin.  Different formulas are required for circular bins and hopper bottom bins. A hopper bottom bin is a cylindrical bin with a hopper at the bottom. The hopper (the conical structure at the bottom) allows farmers to empty bins easily, without having to sweep them out.  

Two hopper bottom bins and an auger.

Volume measurements can be useful in other areas as well, such as finding the volume of a stack of hay.  A question was sent into the Quandaries and Queries section of Math Central that asked about the volume of a hopper.  Farmers encounter these types of questions regularly. 

Suppose a farmer has peas stored in a hopper bottom bin.  The seam on the side of the bin splits, pouring peas onto the ground in a pile.  The farmer contacts the maker of the bin and the company offers to pay for the replacement of the bin and to account for the seed on the ground.  The farmer needs to determine how many bushels of grain are in the pile on the ground.  There are several possible options for the farmer.  If he knew how much was in the bin initially, he could auger out what was left in the bin and determine how many bushels must be on the ground.  If this information is not known, the farmer could calculate the volume of the peas on the ground and convert the measurement to bushels.  A similar solution to this type of problem can be viewed on Math Central. 

Rates show a mathematical relationship between speed and time.  With regards to farming, different augers can move grains at different rates.  It is useful for farmers to have an estimate of how long it will take a number of bushels to be augured into a bin, since time is a critical part of farming.  Most auger rates are given in bushels per minute.  If the farmer knows how many bushels are in the truck, they can estimate the amount of time it will take to unload the truck.  Similarly, if two augers are moving grain into the same bin, the bin will fill up in a substantially shorter amount of time.

These two augers move grain into bins at different rates of bushels per minute.

Seed cleaning plants use mathematics when they clean grain.  When a truck comes into the seed cleaning plant, it is weighed.  The customer is charged for cleaning the seeds according to their weight.  During the cleaning, a sample of seeds is spread onto the table and one hundred seeds are counted out by hand.  The sample must be 99.5% – 99.9% pure, meaning that if 5 kernels are found that are impure, the seed sample is obviously not clean enough.  Even in elevators, samples of grain are counted by hand and inspected for impurities.  The truck is again weighed as it leaves the plant so that the farmer knows how much clean grain he is taking home with him.  Farmers clean their grain for better grades and prices – part of the mathematical model of farming.

A truck loaded with barley.

The math used in farming is sometimes unnoticed.  The calculations and formulas require mathematical knowledge and farmers use their problem solving and money management abilities daily.  Farmers use more advanced math to calibrate machines and irrigation pumps.  Basic geometry, proportions, multiplication, and measurement skills are used everyday by farmers.

Advancements in farming mean faster machinery and less time.  More work can be done with fewer people in a shorter amount of time.  Technology has allowed farmers to increase the size of their operation without increasing manpower.  Years ago, one person could clean 50 pounds of cotton in one day.  With the invention of the Cotton Gin, one person could clean 1000 pounds of cotton in a single day.  This was a significant progression in the way of farming.  Today, new developments and inventions are even more considerable.  Small family farms are becoming larger, with fewer people.  And, as technology increases, so does a farmer’s use for mathematics. 

Bins and an auger located on a farm south of Morse, Saskatchewan, Canada.

References:

Pennsylvania State University. Agronomy Guide 2005 - 2006. Retrieved 24 July 2006, from the World Wide Web. http://agguide.agronomy.psu.edu/agdefault.cfm

Wood, John R.; Wood, Alice Romberg. "Agriculture." BookRags. Retrieved 24 July 2006, from the World Wide Web. http://www.bookrags.com/sciences/mathematics/agriculture-mmat-01.html

Special thank you to Kristen Bestrop of Pioneer Grain, Kelvin Glydon of Reed Lake Seed and Sales, and Ryan Olynick of Olynick Agro, for all of their help and expertise.