Vol. 46, No. 2

Whole Number 152

June 2003

Friezing at Washington State University

by Judith J. McDonald* and J. Harley Weston**

*Department of Mathematics, Washington State University, Pullman, Washington 99163-3113, USA.
**Department of Mathematics & Statistics, University of Regina, Regina, Saskatchewan, Canada, S4S 0A2.
1 Introduction
As mathematicians, we often talk about creativity, elegance and beauty in our work. We look for pattern, structure and form in the objects we're studying. These concepts are more commonly associated with the works of artists and artisans but they are also prevalent in mathematics. One place where the parallels between artistry and mathematics becomes evident is in the mathematical analysis of the structure and symmetry in artistic designs. In this article we will look at frieze designs from a mathematical perspective. Frieze designs are border decorations where a particular pattern is repeated indefinitely in a linear fashion. These designs show up in a variety of mediums in many cultures, from designs on clothing to the ornate architecture of places of worship and public buildings. We see a natural human tendency to use symmetry and repetition to visually enhance our surroundings.

In this article, we will start by determining the functions which map the plane onto itself, preserving the size and shape of any objects represented in it, and mapping a specified line back onto itself. These are the functions which preserves frieze patterns. We will then look at the algebraic structure of this collection of functions under the operation of composition, and show how the seven frieze groups are generated. We illustrate each frieze group algebraically and geometrically. We conclude our article with a tour of the Washington State University campus, looking at the ways in which frieze groups are exhibited and used in our immediate surroundings.

2 Isometries
An isometry of the plane is a function f  which maps the plane onto the plane and preserves distance. A consequence of this distance preserving property is as follows. Consider any two points p and q in the plane. Draw a circle centered at p and going through q. If we draw a circle around f(p) of the same radius, then f(q) must lie on the boundary of this new circle.

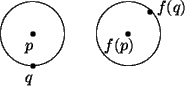
We are interested in all the isometries of the plane which have the additional property that they map a given line $\cal{L}$ back onto itself. For ease of notation, we will assume that our line ${\cal L}$ is the horizontal axis and we describe it by ${\cal L}=\{\ (l_1,0)\ \},$ where l₁ varies over all real numbers. An example of an isometry which maps ${\cal L}$ onto itself is $f(l_1,l_2)=(l_1+5,l_2).$

We classify the isometries f  that map $\cal{L}$ onto itself by looking at the portion of the plane that they leave fixed. There are three cases to consider: f  leaves no point fixed as in the example above, f  leaves exactly one point fixed and f  leaves more that one point fixed.

Suppose first that there is exactly one point, call it p = (p₁, p₂), such that f(p) = p. Let l be the point on $\cal{L}$ which is closest to p.

Since f(l) is on $\cal{L}$ and the only point on $\cal{L}$ which is the appropriate distance from f(p) = p is l itself, it follows that f(l) = l. Since we assumed that p was the only point fixed by f, it must be the case that l = p and hence p is on the line $\cal{L}$, and thus p = (p₁, 0). Let q be any other point on $\cal{L}$. We know that f(q) is on the line $\cal{L}$, Observe that there are only two points on the line $\cal{L}$ which intersect the circle centered at p = f(p) and going through q.

Since f(q)  q it follows that f(q) is the point on the opposite side of p from q. Let r be any point which is not on $\cal{L}$. Then by ensuring that the distance from f(r) to p is the same as the distance from r to p, and that the distance from f(r) to f(q) is the same as the distance and from r to q we see two possibilities for f(r).

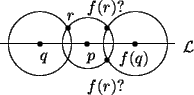
If we take s to be on a line perpendicular to $\cal{L}$ through p, we see that since f(s)  s it must be that f(s) is on the opposite side of the line $\cal{L}$ from s. If we ensure that the distance from r to s is the same as the distance from f(r) to f(s) we see that all the points r not on $\cal{L}$, get mapped to the opposite side of $\cal{L}$. Algebraically,
f(r) = f(r₁,r₂) = (p₁ + (p₁ - r₁ ), - r₂ ) = (2p₁ - r₁, - r₂) for all r = (r₁, r₂) in the plane. Thus this function is a 180 degree rotation R around the point p on the line $\cal{L}$.

Suppose next that there are at least two points p and q which are fixed by f . Then f(p) = p and f(q) = q. Let r be any point on the line from p to q

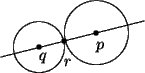
Since f(r) must be the same distance from f(p) = p as r is from p, and the same distance from f(q) = q as r is from q, we see that f(r) = r. Thus if f  fixes more than one point, then it fixes every point along some line.

Consider first the case where f  fixes exactly the line $\cal{L}$, viz. f(l) = l for every l on $\cal{L}$ and f(r)  r for every r not on $\cal{L}$. Let r be any point not on $\cal{L}$ and let p and q be points on $\cal{L}$. Since f(r) must be the same distance from f(p) = p as r is from p and the same distance from f(q) = q as r is from q, and f(r)  r we see that there is only one possibility for f(r).

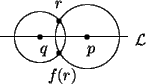
Algebraically we have that f(r) = f(r₁, r₂) = (r₁, -r₂) for every point r in the plane. In this instance our function is a reflection H through the horizontal line $\cal{L}$.

Now consider the case where f  fixes exactly the line where . Let p be any point on but not on . Let l be the closest point on $\cal{L}$ to p. Again since f(l) must be on $\cal{L}$ and it must be the same distance from f(p) = p as l is, we see that f(l) = l.

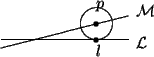
Thus both p and l are on and hence is perpendicular to $\cal{L}$, and intersects $\cal{L}$ at l. Let r be any point which is not on . Since f(r) must be the same distance from f(p) = p as r is from p, and the same distance from f(l) = l as r is from l, and in addition f(r)  r we see that f(r) is uniquely determined.

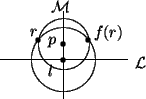
Algebraically, f(r) = f(r₁, r₂) = (l₁+ (l₁ - r₁), r₂) = (2l₁ - r₁, r₂), where l = (l₁, l₂) is the point where intersects ${\cal L}$. This function is a reflection V through the vertical line .

Suppose f  fixes a line and a point r not on . Let p be any point on . Then, as above, the line ${\cal N}$ through p and r is fixed by f. But then the line through any point on ${\cal N}$ and any point on is also fixed by f. In fact, every point in the plane is fixed by f  and hence f  is the identity mapping I.

Our final case to consider is the case where no points are fixed by f . That is, f(r)  r for all points r in the plane. Let p be a point on the line ${\cal L}$. Then p is not fixed by f. Since f(p) is also on ${\cal L}$, it is some distance a units to the right or left of p. We'll consider the case where it is a units to the right of p. The case where it is a units to the left of p is similar. Let q be the midpoint between p and f(p). Then since f(q)  q and the distance between f(p) and f(q) is the same as the distance between p and q, again we see that there is a unique choice for f(q) - it must be a units to the right of q.

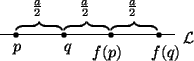
Let l be any other point on the line. By maintaining the appropriate distances between f(l) and f(p) and f(l) and f(q), we see that f(l) must be a units to the right of l. Let r be any point not on ${\cal L}$. Again by maintaining the appropriate distances between f(r) and f(p) and f(r) and f(q), we see that there are two possibilities for f(r):

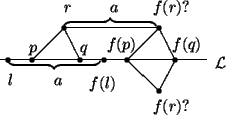
If f(r) is on the same side of ${\cal L}$ as r, then for any other point s in the plane, f(s) must be on the same side of ${\cal L}$ as s. Algebrically we get that f(r) = f(r₁, r₂) = (r₁ + a, r₂) for every point r in the plane. We refer to this function as a translation T.

If f(r) is on the opposite side of ${\cal L}$ from r then for any other point s in the plane, f(s) must be on the opposite side of ${\cal L}$ from s. Algebrically we get that f(r) = f(r₁, r₂) = (r₁ + a, - r₂) for every point r in the plane. We call this function a glide-reflection and denote it by G.

Thus our classification leaves us with six types of functions:

I - the identity where I(r₁, r₂) = (r₁, r₂).

T_a - a translation where T_a(r₁, r₂) = (r₁ + a, r₂).

G_a - a glide-reflection where T_a(r₁, r₂) = (r₁ + a, - r₂).

H - a reflection through the horizontal line ${\cal L}$, where H(r₁, r₂) = (r₁, - r₂).

V_p - a reflection through a line perpendicular to ${\cal L}$ through the point (p, 0) where V_p(r₁, r₂) = (2p - r₁, r₂).

R_m - a rotation of 180 degrees around the point (m, 0) where R_m(r₁, r₂) = (2m - r₁, - r₂).

Notice that T₀ = I, and G₀ = H.

3 Groups of Isometries
If we compose any two of these functions, then necessarily we get back another isometry which maps ${\cal L}$ onto ${\cal L}.$

Let's begin first by looking at what we get if we compose two translations:

$$T_a \circ T_b=T_a(T_b(r_1,r_2))=T_a(r_1+b,r_2)$$

$$=(r_1+a+b,r_2)=T_{a+b}.$$

Thus a translation of a units composed with a translation of b units gives us a translation of a + b units. A set

, together with an operation

on

is said to be closed under

provided that for any two elements U and V in

, the element U 

 V is also in

. The previous argument shows that the set of translations is closed under composition.

Notice that T_a  T₀ = T_a = T₀  T_a. An element E in is called an identity of with the operation provided that for any U in we have U  E = U = E  U. The element T₀ is the identity element of the translations.

Notice next that T_a  T_-a = T_a - a = T₀. If U and V are elements in such that U  V = E = V  U, (where E is the identity of under ), we say that V is an inverse of U. The element T_-a is the inverse of T_a.

So far, we have only composed two functions at a time. What happens if we compose three? Notice that

$$T_a\circ (T_b\circ T_c)=T_a\circ T_{b+c}=T_{a+b+c}$$

and

$$(T_a\circ T_b)\circ T_c=T_{a+b}\circ T_c=T_{a+b+c}.$$

Thus T_a 

 (T_b 

 T_c ) = (T_a 

 T_b )  T_c. We say that an operation on

is associative provided that for any U, V and W in

, U  (V  W) = (U  V)  W. The operation of composition is an associative operation on the set of translations.

What happens if we compose two translations in opposite order. Notice T_a  T_b = T_a + b = T_b + a = T_b  T_a. If for every U and V in , we have U  V = V  U, then we say that the operation on is commutative. Composition is a commutative operation on the set of translations.

A set together with an operation is called a group provided it is closed, contains an identity, every element has an inverse, and the operation is associative. If, in addition, the operation is commutative, we say it is a commutative group. We've seen that the translations form a commutative group under composition.

Now let us look again at the full set of isometries which map ${\cal L}$ onto itself and examine the various compositions of these functions. We can organize these compositions into what is refereed to as a Cayley table. We begin by constructing a six by six table with a row and a column corresponding to each of the six types of isometries which map ${\cal L}$ to ${\cal L}$. The j, k entry in the table represents the function we get by taking the function corresponding to row j composed with the function corresponding to column k. For example the entry in the second (T_b) row and the third (G_c) column is G_b + c = T_b  G_c. The completed Cayley table is shown here:

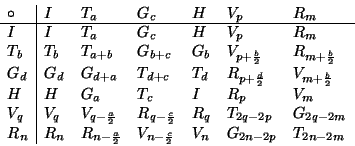
Notice that the composition of any two of these functions is again an isometry which maps ${\cal L}$ onto ${\cal L},$ and hence this set is closed under composition. The function I acts as the identity. By choosing a,b,p,q,m,n correctly, the reader can check that every element has an inverse (recall that T₀ = I). We also leave it to the reader to check that composition is associative. At this point, however, we would like to point out that composition on this set is not commutative. For example, T_a  V_p = V_p + ^a/2 whereas V_p  T₀ = V_p - ^a/2, and hence they are not equal whenever a  0. Thus the set of isometries which map ${\cal L}$ to ${\cal L}$ form a group under composition, but not a commutative group.

A subset of a group which is also a group under the same operation is called a subgroup. Given a collection of elements U₁,U₂,...,U_k, from a group, we denote the smallest subgroup which contains all of these elements by <U₁,U₂,...,U_k>. The set of translations is a subgroup of the group of isometries which map ${\cal L}$ onto ${\cal L}$ under the operation of composition.

Let's begin with a translation of one unit to the right, T₁ What is the smallest subgroup, , which contains this element? It must have an identity, so T₀ = I must be in . The inverse of T₁ namely T_-1 must also be in the set. It inherits associativity from the big group, so the last thing we need to ensure is that it is closed under composition. Since T₁  T₁ = T₂ the function T₂ is in . Similarly T₁  T₂ = T₂ is also in , as is T_-1  T_-1 = T_-2. In fact

 = {T_a| a is an integer}

is the smallest subgroup which contains T₁.

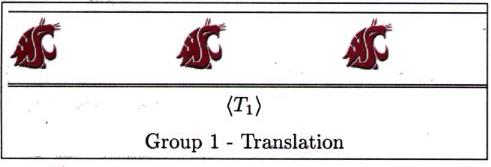
Starting with a blank page (plane) except for one cougar head,

applying each translation from to the plane and shading in the image of the cougar head, we get the pattern:

where the pattern continues forever to the right and to the left.

Going back to our collection of isometries which map ${\cal L}$ to ${\cal L}$, we want to examine the subgroups we can generate taking subsets of the set

{T₁, G₁, H, V₀, R₀}.

Since the identity I is contained in every subgroup, we do not need to include it as one of the subgroup generators. We get a collection of finite subgroups as follows:

$$\langle H \rangle=\{ H,I \}$$

$$\langle V_0 \rangle=\{ V_0,I \}$$

$$\langle R_0 \rangle=\{ R_0,I \}$$

$$\langle H,V_0\rangle =\langle H,R_0\rangle =\langle V_0,R_0\rangle$$

$$=\langle H,V_0,R_0\rangle=\{H,V_0,R_0,I\}.$$

The remaining subgroups generated by possible combinations of the functions from our set generate infinite subgroups. These seven infinite subgroups are the frieze groups.

4 The Frieze Groups
In this section we present the frieze groups both algebraically and geometrically. Each picture represents the pattern you would get (repeated indefinitely to the left and right of course), if you apply every transformation in the subgroup generated by the functions listed, to a single cougar head sitting in the plane.

5 Campus Tour
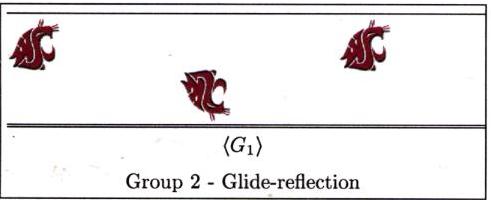
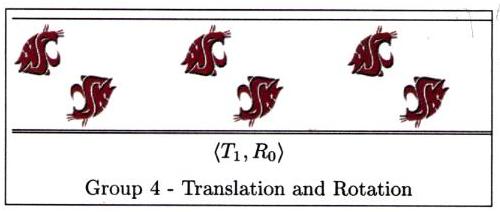
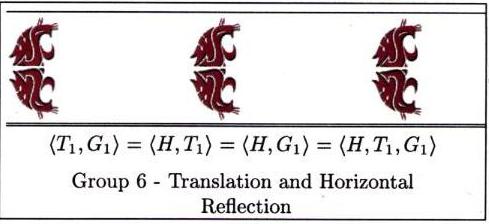
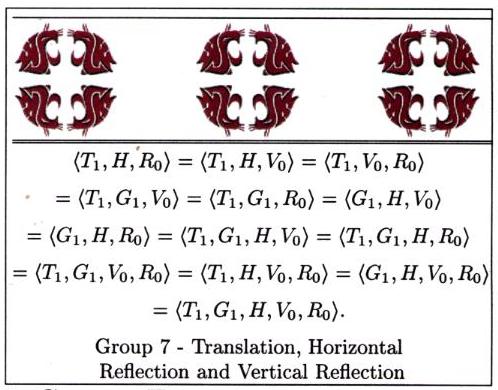
Now it's time to head out for a tour of the campus. We'll look for frieze designs on and in buildings, at the bookie, and even in the parking lots. See if you can classify each of the frieze designs below, and then head out for your own search.

We can see frieze groups on traditional decorations on buildings,

and their railings:

In fact, the basic construction method used on campus forms a nice pattern:

We found some designs showed up out of practicality,

and others had something to do with their functionality.

Wow - the friezing on these tire treads is all from the same group. Notice that they don't have a horizontal or vertical reflection. Interesting!

  

We found some friezing with a bit of a twist

and the clock tower has quite a bit:

We see friezing on art work and jewelry:

Even nature can't resist friezing,

although occasionally even humans can:

Well, we'd best head back to the office, and look here's one last example of a frieze group.

Bibliography

B Jinny Beyer, Designing Tessellations, Contemporary Books, Chicago, Illinois, 1999.

G Joseph A. Gallian, Contemporary Abstract Algebra, D. C. Heath and Company, Lexington, Massachusetts, 1994.

WC D. K. Washburn and D. W. Crowe, Symmetries of Culture: Theory and Practice of Plane Pattern Analysis, University of Washington Press, Seattle, Washington, 1988.

Return to Math Central

To return to the previous page use your browser's back button.