Judi McDonald
Washington State University
and
Harley Weston
University of Regina
Introduction
Frieze patterns or border patterns are commonly found in wallpaper borders, designs on pottery, decorative designs on buildings, needlepoint stitches, ironwork railings and in many other places. In this article, we will describe the seven Frieze designs and illustrate them using the textiles and clothing of the indigenous peoples of North America.
The essential elements are symmetry and repetition.

Lakota (Sioux) blanket band circa 1870
Source: Joel Monture,
The Complete Guide to Native American Beadwork,
McMillan General Reference, 1993

A tile

Decorative trim on a building
The Athapaskan quillwork band above is not a frieze pattern.
There is no block that repeats to form the design.
Source: The Royal Ontario Museum
Frieze patterns can be classified mathematically by the types of symmetries they posess, and this classification gives rise to seven symmetry classes. In this note we examine the symmetry structure in frieze patterns and justify the fact that only seven symmetry classes are possible. We also include examples of each of the seven symmetry classes from art and crafts of the indigenous peoples of North America. In the Teacher notes are activities around frieze designs suitable for students from elementary to secondary school.
Indigenous Art
Below is a gallery of frieze designs we found in the art and crafts of the indigenous peoples of North America. Click on the thumbnail image to see a larger image. In each case we have isolated the portion of the artwork that contains the frieze pattern of interest.
 |
 |
 |
 |
 |
 |
 |
|||
Frieze patterns are formed by functions or actions on the plane that preserve distances. These functions are called isometries. The isometries that generate frieze patterns have the additional property that they map a fixed line, L back onto itself.
To explore these isometries in a concrete way take two transparencies that you would use for an overhead projector, draw a line on each one, and place one on top of the other so that the lines coincide. You need to imagine that each transparency is of infinite length. An isometry that maps the line back onto itself is any action that lifts the top transparency, moves it in any way and then places it back on the bottom transparency with the lines again coinciding. The transparencies do not have to lie directly on top of each other, only the line L. In particular we can slide the top transparecy on the bottom transparency as long as L stays on top of L.
In the diagrams below L is the dark horizontal line. So that we can see the result of moving the top transperency we have placed the letter R in the same position on both transparencies, on one transparency in red and on the other transparency in blue.
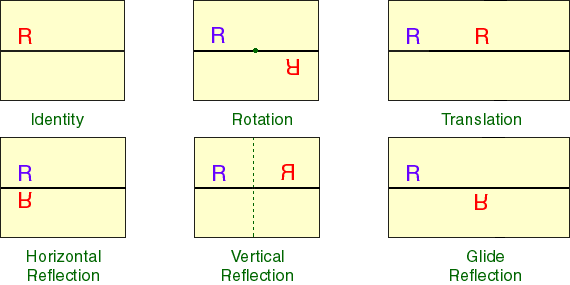
- The diagram labeled Identity is the result of leaving the top transperency unmoved.
- The diagram labeled Rotation is the result of rotating the top transperency 180o, around the point shown in green.
- The diagram labeled Translation is the result of moving the top transparency to the right (or the bottom transparency to the left).
- The diagrams labeled Horizontal Reflection and Vertical Reflection result from the action of turning the top transparency over, either top to bottom or left to right. In the former this is a reflection in the horizontal line L and in the latter a reflection in the vertical, dashed green line.
- Finally the diagram labeled Glide Reflection results from sliding the top transparency to the right and then reflecting it in the line L.
Since these are the only isometries that map L onto itself, frieze patterns must be generated by repeating combinations of these actions. Repeating the action T indefinitely, results in a frieze pattern that we call Pattern 1
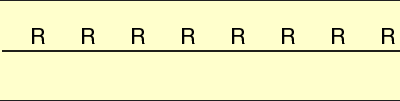
Frieze Pattern 1
Simularly repeating the action G indefinitely also results in a frieze pattern, Pattern 2
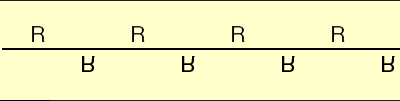
Frieze Pattern 2
In this pattern the tile is
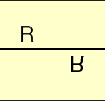
but the pattern is generated from a single R by the repeated action of a glide reflection. This samll piece of the pattern that has no symmetry and generates the entire design by applications of I, R, T, H, V, and G is called a cell.
Repeating any of the other actions does not generate a strip required to be a frieze design. To generate other patterns we are going to have to combine Pattern 1 or Pattern 2 with the other actions. Again this can be done constructively on transparencies. Produce two copies each of Patterns 1 and 2 and, in each case, place one copy on top of the other and then apply one of the other actions on the top transparency.
For example applying the action V to Pattern 1 generates the pattern
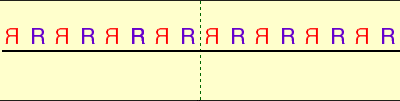
Frieze Pattern 3
which we call Pattern 3. As above the vertical reflection is in the dashed green line.
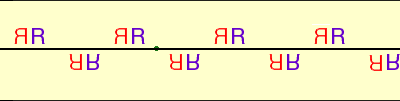
Simularly applying action R by rotating Pattern 1 by 180o around the green dot yields Pattern 4.
Frieze Pattern 4
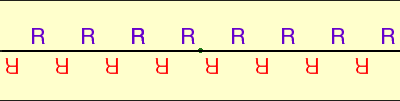
Applying the rotation R to Pattern 2 gives rise to Pattern 5
Frieze Pattern 5
and the horizontal reflection H applied to Pattern 1 gives Pattern 6.
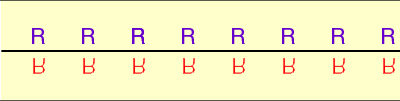
Frieze Pattern 6
We now have to ask if additional patterns arise from applying any of the five isometries to Patterns 3, 4, 5 or 6. Some experimentation shows that the horizontal reflection H applied to Pattern 3 yields Pattern 7.
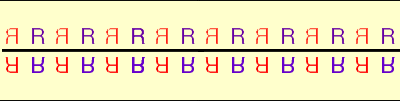
Frieze Pattern 7
Recognition Chart
Classifying a particular frieze pattern as one of the seven patterns can be challenging. The following flow chart, adapted from Gallian, and Washburn and Crowe can be an aid in the classification.
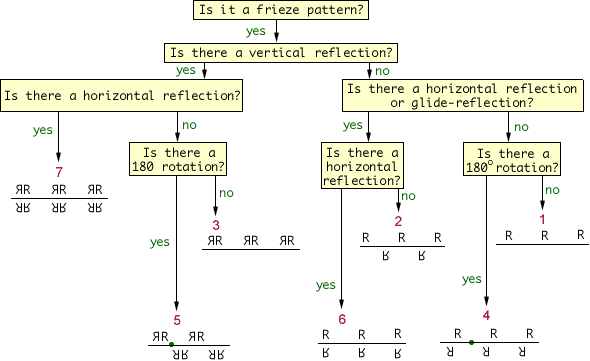
Example
Let's classify the frieze design on the mitten in our Indigenous Gallery.
- Is it a frieze pattern?
Yes. The rectangle outlines the repeated block.

- Is there a vertical reflection?
Yes. There is a vertical reflection in the dashed line.

-
Is there a horizontal reflection?
No. -
Is there a 180o rotation?
Yes. There is a 180o rotation about the dot.

Classify the "The Lakota (Sioux) blanket band"
Classify the "Decorative trim on a building"
References and resources
Joseph A. Gallian, Contemporary Abstract Algebra, D. C. Heath and Company, Lexington Massachusetts, 1994.
D. K. Washburn and D. W. Crowe, Symmetries of Culture: Theory and Practice of Plane Pattern Analysis, University of Washington Press, Seattle Washington, 1988.
Judi McDonald and Harley Weston, Friezing at Washington State University
M. Ascher, Ethnomathematics: A Multicultural View of Mathematival Ideas, Brooks/Cole Publishing Company, Pacific Grove California, 1991.
Frieze Patterns http://www.ucs.mun.ca/~mathed/Geometry/Transformations/frieze.html
Frieze Patterns http://www.joma.org/vol1-2/framecss/rintel/Math/seven.html
Frieze Patterns in Cast Iron. http://www.nrich.maths.org.uk/mathsf/journalf/nov98/art1/
South African Beadwork. http://sunsite.wits.ac.za/math/frieze.htm
Indigenous Mathematics of Central and South America - Mathematics and the
Liberal Arts, http://math.truman.edu/~thammond/history/IndigenousCentralAndSouthAmerica.html