Qu'est ce qu'un angle solide ?? J'ai beau chercher dans mes documents, je ne trouve rien de bien convaincant sur le sujet si ce n'est une définition qui me semble bien vague et creuse ... En vous remerciant de votre attention ( puissiez vous illustrer votre réponse par un exemple, s.v.p...)

Bonjour,
Il y a trois réponses à la question, tout comme il y a trois réponses à la question, "qu'est-ce qu'un angle dans le plan?"

Dans le plan, les trois réponses sont: a. Un ANGLE est une figure formée par un point (nommé le sommet) et deux demi-droites qui partent de ce point. b. Les demi-droites de la définition (a) divise le plan en deux régions, l'une ou l'autre de ces régions pouvant être "l'intérieur". Un ANGLE est l'intérieur de la région du plan entre les deux demi-droites partant du point. c. Le mot angle indique aussi la mesure de la figure décrite en (b): un ANGLE (mesuré en radians) est la longueur de la portion du cercle unitaire qui se trouve à l'intérieur de l'angle lorsque le cercle est centré au sommet de l'angle. Dans le diagramme, la longueur de l'arc orange est la mesure du plus petit angle et la longueur de l'arc vert est la mesure du plus grand angle. Dans les deux cas, l'unité de mesure est le radian.

Dans les trois dimensions, les réponses sont: a. Un ANGLE SOLIDE est la figure formée par toutes les demi-droites partant d'un point (nommé le sommet) et passant à travers tous les points d'une courbe fermée (telle qu'un cercle ou un polygone). On peut imaginer un angle solide comme étant une pyramide (ou un cône) n'ayant aucune base. b. Un ANGLE SOLIDE est l'espace limité par toutes les demi-droites de (a).   c. L'expression "angle solide" indique aussi la mesure de l'objet décrit dans (b): un ANGLE SOLIDE (mesuré en stéradians) est l'aire de la portion du cercle unitaire délimité par l'angle quand son sommet est au centre de la sphère.

EXAMPLES

1.	Le coin d'une pièce, où les deux murs sont perpendiculaires l'un à l'autre et au plancher, forme un angle solide familier (on utilise un triangle comme courbe fermée dans le diagramme). Puisque (I) l'angle enlève 1/8 de la sphère et (ii) que l'aire de la sphère-unité est 4*pi, sa mesure est pi/2 stéradians.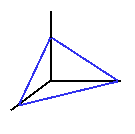
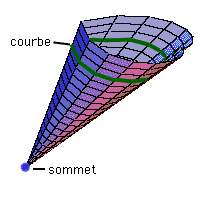
Dans le deuxième exemple, nous avons un angle solide dont les côtés sont "plats" (c'est-à-dire, les côtés sont des angles ordinaires dans le plan). Avant d'aborder l'exemple, rappellons-nous que l'ANGLE DIEDRE entre deux plans qui se croisent est égal à la mesure de l'angle formé par les lignes d'intersection des plans donnés et un plan qui leur est perpendiculaire. Une autre façon de regarder l'angle dièdre: imagine les plans qui forment l'angle se croisant avec la ligne qui joint le pôle nord d'une sphère à son pôle sud. La mesure de l'angle dièdre est donc la longueur de l'arc coupé à l'équateur. Nous avons besoin d'angles dièdres pour parler des angles d'un polygone sphérique. Un POLYGONE SPHERIQUE a ses n sommets sur la sphère; ses côtés sont formés par les arcs des cercles centrés au centre de la sphère et qui joignent les sommets consécutifs. L'angle entre les côtés consécutifs du polygone est l'angle dièdre entre les plans des cercles qui forment ces côtés.
2.	Regardons n'importe quel polygone à n côtés; la somme de ses angles est (n-2)*pi. Joignons un point qui n'est pas dans le plan du polygone aux points sur les côtés du polygone; les côtés de l'angle solide qui en résulte sont les angles n du plan qui sont formés. La mesure de cet angle solide est égal à l'aire du polygone sphérique que l'angle coupe dans la sphère unitaire. THEOREME. L'aire d'un polygone sphérique à n côtés est égal au surplus de la somme de son angle moins la somme de l'angle d'un polygone à n côtés dans le plan: si les angles dièdres entre côtés consécutifs sont A, B, C, ...,l'aire du polygone sphérique est donc A+B+C+...- (n-2)*pi. De même, nous voyons que l'angle solide de l'exemple 1 mesure 3*(pi/2) - (3-2)*pi = pi/2 stéradians.

Au revoir,
Chris