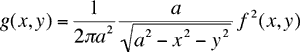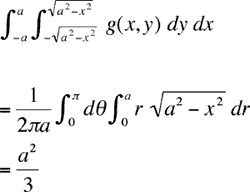Nom : jennifer
Etudiante
Je vous serais très reconnaissante si vous pouviez
m'expliquer :
pourquoi la moyenne des projections quadratiques d'un segment sur un
axe (en 3D) est égale à a*a/3 sachant que "a" représente
la longueur de ce segment et que toutes les orientations du segment sont également
probable.
En
vous remerciant
et bravo pour votre site!
jennifer
Jennifer.
Qu'est-ce que vous voulez dire au juste par "projections quadratiques d'un segment sur un axe''? La formule a2/3 depend des unites: pour un segment de 100 centimetres ca donne une valeur de 10000/3 > 100 tandis que pour un segment de 1 metre ca donne une valeur de 1/3 < 1, ce qui me donne a penser que si la formule est juste, il s'agit d'une mesure d'aire plutot que d'une mesure de longueur.
Claude
Soit un segment de longueur "a" effectuant un angle "teta" avec une droite. sa projection sur cette droite est donnée par : a*cos(teta) Donc sa projectrion au carré est donnée par : (a*cos(teta))2
sachant que toutes les orientations de ce segment par rapport à la droite sont également probable, et que l'on se place dans le cas 3-dimensions, pourriez-vous m'expliquer pourquoi la moyenne de toutes les projections au carré de ce segment sur cette axe est : a*a/3.
merci
jennifer
Ce qui est difficile à modéliser, c'est "l'axe aléatoire''. On veut d'abord simplifier ce modèle. Soit donc S, un segment fixe de longueur a et A un axe d'orientation aléatoire.
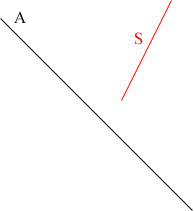
On peut alors coller A à une extrémité de S, ramener le
point d'intersection à
l'origine puis effectuer une rotation (sans changer l'angle) de façon à rendre
A
vertical et l'autre extrémité de S sur la sphère de rayon
a centrée à
l'origine.
Qui plus est, on peut supposer que l'extrémité de S est sur l'hémisphère
supérieur
plutôt que sur l'hémisphère inférieur.
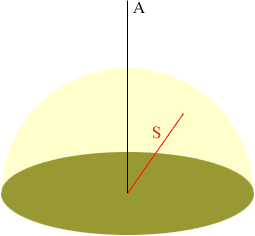
Cette transformation effectuée, c'est l'axe vertical A qui devient fixe
et
l'orientation
du segment S qui est aléatoire: S est maintenant un segment reliant l'origine
à
un point
choisi aléatoirement sur l'hémisphère supérieur de
rayon a centré à l'origine.
Le calcul de la moyenne des projections quadratiques suit ensuite les règles
du calcul de l'espérance en probabilité. La valeur de la projection
au point dont les deux premières coordonnées sont x et y est donnée
par
,
et la valeur de la projection quadratique à ce
point est f2(x,y).
Pour trouver l'espérance de cette valeur on multiplie f2(x,y)
par la "densité'' au point (x,y,f(x,y)) qui est
sqrt{1 + ( df/dx)2 + ( df/dy)2},
pondérée par l'aire de l'hémisphère,soit
2![]() a2.
Tout calcul fait, on
obtient
a2.
Tout calcul fait, on
obtient
à intégrer sur toutes les valeurs (x,y) telles que x2 + y2 <= a2, ce qui donne une projection quadratique moyenne de
J'aimerais bien pouvoir donner une validation moins laborieuse et plus
intuitive,
mais je ne sais pas s'il en existe une.
Claude