Nous décrivons ici un problème ouvert en géométrie au sujet des réflections de triangles.Ce problème est la source du graphique ci-haut, qui est l'image de fond de l'affiche "Mathématiciens au Travail". Quand Judi et Harley cherchaient une image de fond pour l'affiche, Nathalie leur a montré le problème et l'algorithme qui produit le graphique.

Partant d'un triangle ABC, on réfléchit chaque sommet à travers le
côté opposé, ce qui donne un nouveau triangle A₁B₁C₁ -- le premier triangle réfléchi.

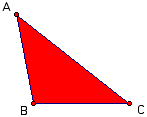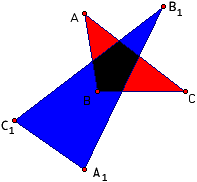Quelle relation y-a-t'il entre ABC et A₁B₁C₁? Lorsque ABC est isocèle, A₁B₁C₁ l'est aussi,

et lorsque ABC est équilatéral, A₁B₁C₁ l'est aussi. Peut-être pouvez-vous vérifier ces deux énoncés par vous-même. Supposons maintenant que, tout en maintenant B et C fixes, on déplace A pour modifier la forme du triangle ABC. Alors la forme du triangle A₁B₁C₁ change aussi. Si votre fureteur supporte Java, vous pouvez ouvrir une nouvelle fenêtre qui vous permet de déplacer A, B ou C et voir les modifications du triangle réfléchi.

Des deux triangles ABC et A₁B₁C₁, c'est souvent le second qui ressemble le plus à un triangle équilatéral. Nous avons besoin d'une mesure précise qui reflète cette "ressemblance à un triangle équilatéral". En fait, il existe plusieurs façons de procéder, en mesurant à quel point les angles sont éloignés d'une mesure de 60 degrés ou à quel point les longueurs des côtés sont inégales. La mesure que nous allons utiliser est le rapport du carré du périmêtre à l'aire. Selon un théorème de géométrie, ce rapport est minimal lorsque le triangle est équilatéral; sa valeur est alors 12 sqrt(3), soit environ 20.7.

En plus du triangle A₁B₁C₁ obtenu à partir de ABC par réflections, nous allons aussi considérer A₂B₂C₂ obtenu à partir de A₁B₁C₁ par réflections, A₃B₃C₃ obtenu à partir de A₂B₂C₂ par réflections et ainsi de suite. Ces constructions s'appellent respectivement première itération, deuxième iteration, troisième itération, du processus de réflection. Voici deux images montrant trois triangles réfléchis, la seconde est obtenue de la première en déplaçant le point A légèrement à droite. Si votre fureteur supporte Java, vous pouvez ouvrir une nouvelle fenêtre qui vous permet de déplacer les points A, B, C et observer l'effet sur les triangles réfléchis.

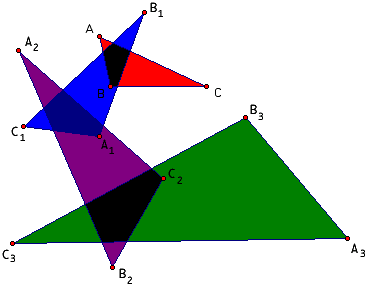
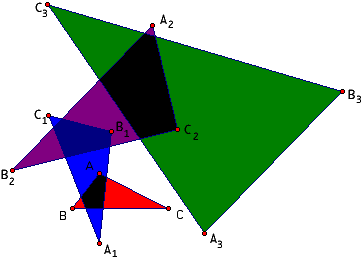
Au début, il était conjecturé que quelque soit le triangle ABC, la suite de triangles A₁B₁C₁, A₂B₂C₂, A₃B₃C₃, ... s'approcherait toujours d'un triangle équilatéral (Schwartz). Comme c'est habituellement le cas en recherche mathématique, certaines personnes s'affairèrent alors à démontrer la conjecture ou à trouver des contre-exemples. Keith Dean a démontré que si les angles de ABC ont un rapport de 1:2:4 (c'est à dire qu'ils mesurent respectivement 25 ⁵/₇, 51 ³/₇ et 102 ⁶/₇ degrés), alors les angles de A₁B₁C₁ ont exactement les mêmes mesures et ainsi, les triangles itérés ne s'approchent pas d'un triangle équilatéral. Par conséquent, la conjecture initiale est fausse. Patrick Callaghan a ensuite donné une charactérisation des triangles ABC tels que les points A₁, B₁ et C₁ sont colinéaires, ce qui donne de nouveaux contre-exemples à la conjecture.

Le problème est donc le suivant:

“Quels sont les triangles ABC pour lesquels la suite de triangles
itérés s'approche d'un triangle équilatéral?”

Nathalie a conçu une méthode qui permet de "voir'' plusieurs cas en même temps. C'est de cette méthode qu'est tirée l'image de fond de l'affiche "Mathématiciens au Travail".

On fixe la base BC du triangle et on choisit le point A quelque part dans le plan. Puis, on itère le processus de réflection deux fois, et on observe à quel point le triangle A₂B₂C₂ s'approche d'^etre équilatéral. Si A₂B₂C₂ est presque équilatéral, le point A est colorié bleu, et sinon, A est colorié blanc. Cette procédure est répétée à tous les points d'une région rectangulaire du plan pour générer le graphique ci-dessous.

Deux itérations¹

De grandes parties du graphique sont en bleu. Si A est dans une de ces parties alors A₂B₂C₂ est presque équilatéral. Par contre, si A est dans une partie blanche du graphique, A₂B₂C₂ est loin d'être équilatéral.

Lorsqu'on itère le processus de réflection trois fois et qu'on colorie le point A en bleu si A₃B₃C₃ est presque équilatéral, on obtient l'image suivante, qui s'apparente à la précédente, sauf que les motifs blancs sont plus complexes.

Trois itérations¹

En itérant le processus de réflection quatre fois, on obtient le graphique suivant, qui a encore plus de bleu et moins de blanc. Il semble donc que la proportion des triangles initiaux qui donnent lieu à des triangles réfléchis presque équilatéraux augmente à mesure qu'on itère le processus de réflection.

Quatres itérations¹

On peut maintenant se poser plus de questions à propos de ces images.Est-ce qu'avec suffisamment d'itérations, toute l'image va devenir bleue? En fait, la réponse est non, puisqu'on sait qu'il existe des configurations initiales pour lesquelles les triangles réfléchis ne convergent pas vers un triangle équilatéral. Les régions correspondant à ces triangles vont demeurer blanches. Vous pouvez vous servir de l'applet du lien ci-haut pour découvrir des triangles ABC pour lesquels la suite de triangles itérés semble converger vers un segment. Pourquoi y-a-t'il d'autres régions blanches? Pouvez-vous trouver d'autres positions pour le point A, ou d'autres conditions qui donnent une suite de triangles qui ne converge pas vers un triangle équilatéral? Est-ce que ces images aident à chercher une solution à la question initiale "Quels sont les triangles ABC pour lesquels la suite de triangles itérés s'approche d'un triangle équilatéral?" L'infographie peut nous aider à développer notre intuition face à ce type de problème, mais une solution complète nécessite une démonstration mathématique.

Si vous trouvez quelque chose d'intéressant en explorant ces questions, faites-nous le savoir à . Nous pourrons peut-être ajouter votre nom à la liste de gens qui ont contribué à faire progresser nos connaîssances vers une solution du problème.

En août 2006, nous avons reçu les informations suivantes de Pasquale Nardone.

 ¹ Les graphiques sont de Matthew McKague

Références

 

Judah Schwartz, "Can technology help us make the mathematics curriculum intellectually stimulating and socially responsible?" International Journal of Computers for Mathematical Learning, 4,1999, pages 99-119.

Nicholas D. Kazarinoff, Geometric Inequalities, Random House, New York, 1961.

La Centrale des maths